저번 포스팅에 바로 이어서, 파이썬 운송 최적화 부분을 마무리해봅니다.
✔Table of Contents
Tech 62. 앞서 구한 최적 운송 경로를 네트워크 시각화하자.
이전에 배웠던 네트워크 시각화를 한번 해봅시다!
공장(F), 창고(W) 좌표정보를 가져와 찍고, 운송경로의 최적해 값(v1)을 엣지의 가중치로 보면, 어떤 운송경로가 두드러지는지를 한 눈에 파악해볼 수 있겠죠?
또한, 이전 6장에서 했던 네트워크와 결과가 어떻게 달라지는지도 확인해 봅시다. (네트워크 시각화가 무엇인지 궁금하다면, 여기에서 확인하세요!)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
#데이터 불러오기
df_tr = df_tr_sol.copy() #가중치이자 최적해(v1)
df_pos = pd.read_csv('7장/trans_route_pos.csv') #좌표
display(df_tr, df_pos)
이렇게 좌표정보인 df_pos, 가중치로 설정할 최적해 df_tr 데이터셋을 가져왔습니다.
가중치를 반영하기 전 시각화를 해봅시다. (참고로 책의 코드보단 제 코드가 더 간단해서 제 코드를 사용했습니다.)
########### 가중치 반영 전 ##############
#객체
G = nx.Graph()
#노드 설정(W 3개, F 4개)
for i in range(len(df_pos.columns)):
G.add_node(df_pos.columns[i])
#엣지 설정(W에서 하나 - F에서 하나를 연결)
for i in range(0, 3):
for j in range(3, len(df_pos.columns)):
G.add_edge(df_pos.columns[i], df_pos.columns[j])
#좌표 설정
pos = {}
for i in range(len(df_pos.columns)):
node = df_pos.columns[i]
pos[node] = (df_pos[node][0],df_pos[node][1])
#그리기
nx.draw(G, pos, with_labels=True)
plt.show()
위 코드는 6장에서 쓴 코드와 거의 비슷하므로 설명은 생략하겠습니다. 네트워크 시각화 포스팅에 자세히 설명해 두었습니다 :)
이젠 엣지의 가중치를 추가해봅시다.
####### 가중치 추가 ########
sy = []
size = 0.1 #가중치 값이 너무 커서 줄임 (그대로 쓰면 엣지가 엄청 굵게나옴)
for i in range(len(df_tr.index)):
for j in range(len(df_tr.columns)):
sy.append(df_tr.iloc[i,j]*size)
sy
엣지에 설정할 가중치는 df_tr에 있는 값을 하나씩 뽑아 'sy' 라는 리스트에 담았습니다.
그리고 df_tr 값을 그대로 쓰면 너무 커서 이 값에 0.1을 곱해서 사용합니다.
#그래프 다시 그리기
nx.draw(G, pos, with_labels=True,
font_size = 16, node_size = 1000, node_color = 'k', font_color= 'w', width = sy) #width에 가중치 리스트 설정
plt.show()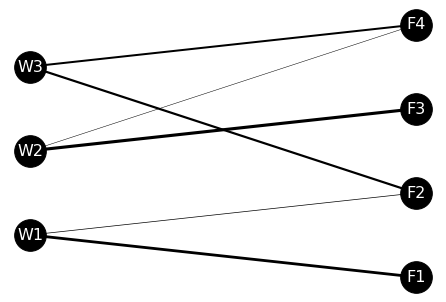
결과는 요렇게 그려지네요!
6장에서 최적화를 반영하기 전과 어떻게 달라졌는지 확인해볼까요?
이렇게 네트워크 시각화를 직접 해보니, 확연히 그림이 달라진 게 느껴지시죠?
얇은 선이 사라지고, 대신 굵은 선은 더 굵어졌습니다. → 즉, 집중할 경로에 더 집중하고, 집중할 필요가 없는 경로는 아예 제거해버렸네요!
결과를 보면 W1 → F1, W2 → F3, W3 → F4, F2 로의 이동이 대부분입니다.
이로써 "운송 경로는 어느 정도 집중되어야 한다." 는 가설이 최적화 계산에 의해 입증되었습니다!
Tech 63. 우리가 구한 최적 운송경로가 제약 조건도 만족하는지 확인하자
여기서 제약 조건을 검사하는 함수는 6장에서 만든 계산 함수를 그대로 가져와 사용합니다.
코드에 대한 자세한 설명은 하지 않으니, 궁금하신 분들은 [이 포스팅]을 참고하세요! (Tech 59, 60번)
#필요한 데이터
import pandas as pd
import numpy as np
df_demand = pd.read_csv('7장/demand.csv')
df_supply = pd.read_csv('7장/supply.csv')
display(df_demand, df_supply)
필요한 수요, 공급조건 데이터를 불러옵니다. 그리고 6장에서 만든 함수를 그대로 가져오겠습니다.
## 6장에서 만든 함수 그대로 가져옴
#제약조건 함수화 -> 앞서 만든 if문에서, 수요(or 공급)을 만족하면 1, 아니면 0을 출력하도록 하는 flag를 만든다.
## 먼저 0으로 초기화시키고, 만족하는 경우엔 1을 넣어주기
## 공장(F)의 수요
def c_demand(df_tr, df_demand):
#초기화
flag = np.zeros(len(df_demand.columns))
#계산
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]])
if temp_sum >= df_demand.iloc[0][i]:
flag[i] = 1
return flag
## 창고(W)의 공급
def c_supply(df_tr, df_supply):
#초기화
flag = np.zeros(len(df_supply.columns))
#계산
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]])
if temp_sum <= df_supply.iloc[0][i]:
flag[i] = 1
return flag
위 함수 c_demand와 c_supply는 각각 수요조건, 공급조건을 만족하는지를 계산하는 함수입니다.
만족할 경우 1, 아니면 0을 출력하는 함수입니다.
결과를 보면, 다음과 같이 수요와 공급 모두에 대해서 1이 출력됨으로써 제약조건을 잘 만족시켰음을 알 수 있죠!
즉, 최소수요보단 많이, 최대공급보단 적게 상품이 운송되고 있습니다.
이렇게 함수화하지 않고도, 제약조건을 만족하는지 눈대중으로 파악할 수도 있습니다.
바로 직전 포스팅에서 만든 다음 사진을 참고하면요!
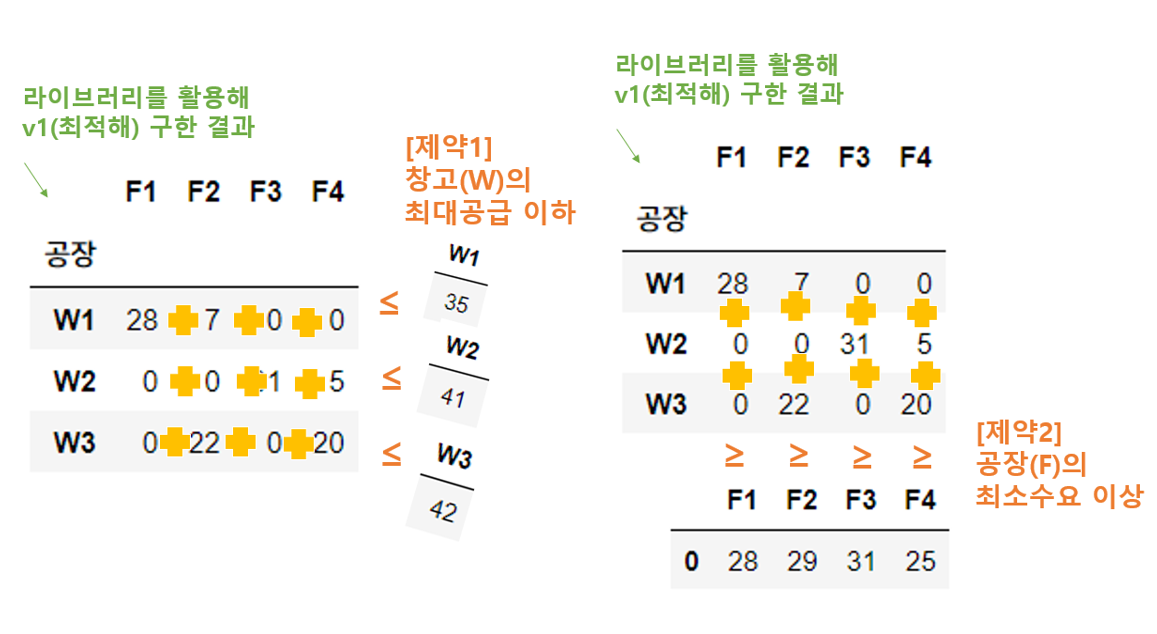
눈대중으로 훑어봐도, 창고의 최대공급 이하 / 공장의 최소수요 이상을 만족함을 확인할 수 있습니다.
Summary
이렇게 목적함수와 제약조건만 명확하게 정의할 수 있다면, 힘들게 데이터를 일일이 바꿔가면서 조건을 만족하는지 확인하지 않고, 최적화 라이브러리를 활용해 간단히 해답을 찾을 수 있습니다. 정말 편리하죠!
최적화 문제엔 다양한 종류가 있고, 모든 최적화 문제가 반드시 정답이 있진 않습니다.
하지만 오늘 살펴본 '운송 최적화'처럼 선형 최적화의 경우, 관련 연구나 라이브러리가 많이 있어 비교적 빠르게 정답을 찾을 수 있습니다.
다음 포스팅은 '운송 비용 최적화'가 아니라, '생산 계획 최적화'를 해봅니다.
지금까진 운송비용을 최소화시키는 최적의 경로를 찾았다면, 목표가 달라집니다.
가장 최대의 이익을 내기 위해, 어떤 물품을 얼마나 만들 것인가? 라는 문제에 대해 최적의 값을 찾아봅니다.
정말 재밌는 문제죠? 다음 포스팅에서 뵐게요!
