Yours Ever, Data Chronicles
물류 네트워크 최적화 설계 예제 (python logistics_network) / 파이썬 데이터 분석 실무 테크닉 100 본문
물류 네트워크 최적화 설계 예제 (python logistics_network) / 파이썬 데이터 분석 실무 테크닉 100
Everly. 2022. 4. 30. 11:55안녕하세요 Everly입니다.
오늘은 [파이썬 데이터 분석 #7장]의 마지막 내용인 '물류 네트워크 설계'에 관해 포스팅해보겠습니다.
우리가 앞서 배웠던 최적화 2가지는 이것이었죠.
이렇게 운송 경로 최적화에서는 운송비용을 최소화하는 최적의 경로를 찾았고, 생산계획 최적화에서는 총이익을 최대화할 수 있는 최적의 생산량을 찾았습니다.
하지만 실제 현장에서는 이 2가지 최적화 기법을 따로 하는 게 아니라, 동시에 고려해야 합니다. 즉, 최적의 '물류 네트워크'를 만들어야 한다는 것이죠. 이런 과정을 통해, 우리는 최적의 운송량과 최적의 생산량 두가지를 모두 만족하는 네트워크를 만들어봅니다.
python ortoolpy 라이브러리의 logistics_network를 이용해 진행해봅니다. 이번 장은 따로 데이터셋을 가져오지 않고 간단히 만들어 사용합니다.
✔Table of Contents
Tech 68. 물류 네트워크 설계 문제를 풀어보자. (ortoolpy logistics_network)
간단한 데이터셋을 만들어봅시다.
import numpy as np
import pandas as pd
제품 = list('AB')
대리점 = list('PQ')
공장 = list('XY')
레인 = (2,2)
print(제품, 대리점, 공장, 레인)
간단하게 제품은 A, B, 대리점(제품을 판매하는 곳)은 P, Q,
공장은 X, Y가 있다고 해봅시다. 공장 내의 레인은 2개가 있습니다.
그 다음부터는 운송비용(편의상 '운송비'), 수요량, 생산비용('생산비'), 생산량에 대해 임의의 값을 만들어 데이터셋을 만들어봅니다. 이 부분은 따로 설명할 게 없으니 설명 없이 넘어갑니다.
# 대리점 - 공장 간 운송비용
trans_cost = pd.DataFrame( ((j,k) for j in 대리점 for k in 공장), columns = ['대리점', '공장'])
trans_cost['운송비'] = [1,2,3,1]
trans_cost
# 각 대리점에서의 제품 수요량
s_demand = pd.DataFrame( ((j, i) for j in 대리점 for i in 제품), columns = ['대리점', '제품'])
s_demand['수요량'] = [10, 10, 20, 20]
s_demand
# 각 공장에서의 제품 생산비용과 생산량(하한: 최소생산량, 상한: 최대생산량)
supply_cost = pd.DataFrame( ((k, l, i, 0, np.inf) for k, nl in zip(공장, 레인)
for l in range(nl) for i in 제품),
columns = ['공장', '레인', '제품', '하한', '상한'])
supply_cost['생산비'] = [1, np.nan, np.nan, 1, 3, np.nan, 5, 3]
supply_cost.dropna(inplace=True)
supply_cost.loc[4, '상한'] = 10 #4번 인덱스만 상한 설정
supply_cost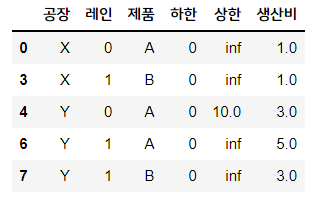
이렇게, 각 데이터셋이 만들어졌습니다. 운송비용, 생산비용, 그리고 수요량과 생산량 데이터가 만들어졌죠.
자, 여기서 이미 고정되어 있어서 우리가 바꿀 수 없는 것은 무엇일까요?
→ 맞습니다. 운송비용, 생산비용과 수요량은 fixed되어 있어 우리가 어찌할 수 없는 것입니다.
반대로 말하면, 생산량은 우리가 바꿀 수 있는 것입니다!
또한 운송량을 어떻게 분배할지도 우리가 바꿀 수 있는 것이죠!
→ 즉, '최적 생산량'과 '최적 운송량' 을 최적화 문제로 찾아봅시다.
from ortoolpy import logistics_network
_, trans_cost2, _ = logistics_network(s_demand, trans_cost, supply_cost,
dep = '대리점', dem = '수요량', fac = '공장', prd = '제품',
tcs = '운송비', pcs = '생산비', wb = '하한', upb = '상한')
display(supply_cost, trans_cost2)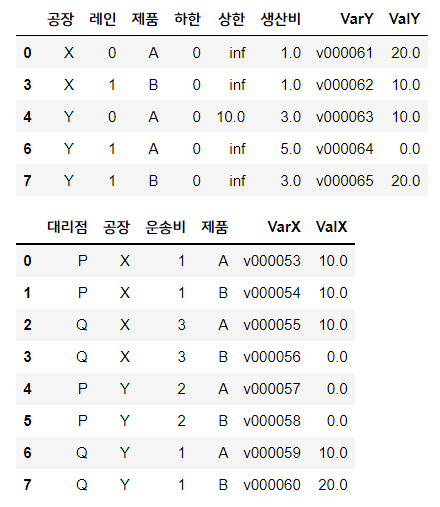
ortoolpy의 logistics_network를 사용해 최적화한 모습입니다.
필요한 데이터셋을 집어넣고, 변수를 지정해주면 위와 같이 결과가 뽑힙니다.
이렇게 해서 만들어진 최적해(optimal solution)은 다음과 같습니다.
- supply_cost의 ValY: 최적 생산량
- trans_cost2의 ValX: 최적 운송량
이제 다음 단계에서 이렇게 뽑힌 최적 생산량과 운송량이 타당한 결과인지 검증해봅시다.
Tech 69. 최적 운송량 검증
#보기 쉽게 데이터프레임 재구성 (tc2 데이터)
tc2 = trans_cost2[['공장', '대리점', '운송비', '제품', 'VarX', 'ValX']]
tc2
먼저, 최적 운송량부터 검증해봅니다.
최적 운송량이 계산된 trans_cost2 데이터프레임을 보기 쉽게 'tc2' 로 순서를 바꿔 재가공했습니다.
여기서 'ValX' 라는 변수가 최적 운송량으로 뽑힌 것이죠.
자, 이제 ValX가 최적의 운송량인지를 어떻게 알 수 있을까요? 바로 '총 운송비용'을 계산해보면 되겠죠!
총 운송비용은 각 경로별 운송비용*운송량으로 계산 → 즉, 각 경로별 운송비*ValX로 계산합니다.
#이 최적의 운송량(ValX)일 때의 총 운송비용은? -> ValX와 운송비를 곱하면 되겠지?
trans_cost = 0
for i in range(len(tc2.index)):
trans_cost += tc2['운송비'].iloc[i]*tc2['ValX'].iloc[i]
print(trans_cost)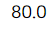
총 운송비용은 80만원입니다. 데이터프레임을 보면 운송비가 적은 X-> P, Y-> Q 등의 경로에 운송량이 많이 배치되었음을 확인할 수 있습니다.
아쉽게도 최적화 전에 운송량이 얼마였는지의 값을 알면, 총 운송비용으로 최적화 전과 후를 비교할 수 있을 텐데 이 데이터에는 최적화 전 운송량 정보가 없습니다. 그래서 그냥 지금 총 운송비용이 80만원이 드는구나! 정도로 만족해야 할 것 같네요.
책에는 없지만, 운송경로를 네트워크 시각화해봤습니다. 좌표정보가 없어 임의로 설정을 했고, ValX를 엣지 가중치로 설정해 시각화했습니다. 따로 설명은 생략합니다. (네트워크 시각화가 뭔지 궁금한 분들은 이 포스팅을 참고하세요)
#운송량을 시각화하기 위해 임의로 공장-> 대리점으로 간 운송량만 더해본다. (사실 어떤 제품을 생산했는지까지 고려해야 하는데 그냥 간단히 보는 목적이니까 생략)
tc3 = pd.DataFrame(tc2.groupby(['공장', '대리점'], as_index=False)['ValX'].sum())
tc3
#네트워크 가시화하기
import networkx as nx
import matplotlib.pyplot as plt
#그래프 객체 설정
G = nx.Graph()
#노드 설정
sy = ['X', 'Y', 'P', 'Q']
for i in range(len(sy)):
G.add_node(sy[i])
#엣지 설정(공장에서 하나 - 대리점에서 하나를 연결)
for i in range(0,2):
for j in range(2,4):
G.add_edge(sy[i], sy[j])
#엣지 가중치 리스트화
size = 0.5 #가중치 사이즈 축소
sy2 = []
for i in range(len(tc3.index)):
sy2.append(tc3['ValX'].iloc[i] *size)
#좌표 설정(정보가 없어 내가 임의로 설정함)
pos = {}
pos['X'] = (0, 0.9)
pos['Y'] = (0, 0.3)
pos['P'] = (0.7,1.3)
pos['Q'] = (0.7, 0)
#그리기
nx.draw(G, pos, with_labels=True,
font_size = 16, node_size = 800, node_color= 'k', font_color = 'w', width = sy2) #가중치는 width 옵션으로 지정
plt.show()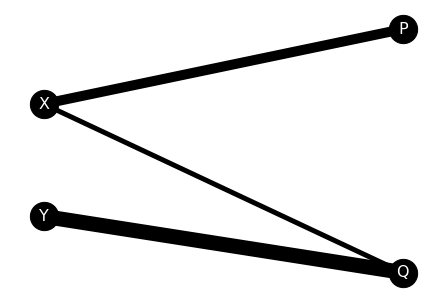
이렇게 networkx 라이브러리로 네트워크 시각화를 해보니, 어떤 경로에 운송량이 많이 배치되었는지를 파악하기가 쉽죠? Y->Q , X->P로 가는 경로에 운송량이 몰빵되었네요. (역시 운송비용을 줄이려면 몰빵을 해야 합니다,,)
Tech 70. 최적 생산량 검증
supply_cost
다음으로는 이 생산량이 최적인가? 를 따져보기 위한 최적 생산량 검증을 해봅니다.
supply_cost 데이터의 ValY에 최적 생산량 값이 구해졌다고 했었죠.
이 때도 마찬가지입니다. 어떻게 얘가 최적 생산량인지 알 수 있을까요? 바로 '총 생산비용'을 구하면 됩니다.
총 생산비용은 제품당 드는 생산비용*생산량의 합이므로 → 각 제품당 생산비*ValY 를 계산하면 되겠죠?
#이 최적의 생산량(ValY)일 때 총 생산비용은? -> ValY와 생산비를 곱하면 되겠지?
product_cost = 0
for i in range(len(supply_cost.index)):
product_cost += supply_cost['생산비'].iloc[i]*supply_cost['ValY'].iloc[i]
print(product_cost)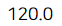
결과를 보면 총 생산비용은 120만원입니다.
데이터프레임을 보면, 생산비용이 낮은 공장X에서의 생산량을 늘렸고,
공장Y에선 레인 1 사용시 생산비용이 5로 가장 높기 때문에 아예 생산하지 않고, 대신 레인 0에서 10개를 생산하는 것으로 최적화되었네요!
이 또한 최적화 전과 후의 총 생산비용 합계를 계산해보면, 생산량 최적화가 잘 되었는지를 확인할 수 있었을 텐데
아쉽게도 최적화 전엔 생산량이 몇이었는지가 정확히 나와있지 않아서(상한/하한만 나와있음) 비교를 할 수 없네요. 현장에선 생산량 정보가 있을 테니 응용할 때 꼭 검증을 해보시길 바랍니다!
+) 참고로, supply_cost를 보면, 공장 X가 생산비용이 적으므로 공장X에서만 생산하면 가장 생산량을 최적화하는 것이 아니냐? 라고 할 수도 있습니다.
하지만 앞서 말했듯, 우리는 생산비용뿐 아니라 운송비용까지 2가지를 모두 고려해야 합니다.
공장 Y에서 대리점까지의 운송비용이, 공장 X에서 대리점까지의 운송비용보다 낮은 경우가 있기 때문에, logistics_network가 이를 고려하여 공장 Y에서도 생산을 일부 하도록 결과를 뽑아준 것입니다. (그래서 결과적으로 공장 Y에선 제품 A 생산을 10, 제품 B 생산을 20만큼 하는 게 최적의 생산량으로 도출되었습니다.)

Summary
이렇게 하여 [파이썬 데이터 분석 #7장]의 최적화 문제를 마칩니다. 여기선 생산계획 최적화, 운송비용 최적화를 다뤘고 마지막으로 물류 네트워크 전체를 최적화하는 방법까지 다루었습니다.
라이브러리를 활용하면 비교적 수월하게 최적화 문제를 풀 수 있지만, 이 결과를 그대로 받아들이면 안됩니다. 최적화 라이브러리를 사용하는 것은 최소의 과정이고, 이게 잘 되었는지 꼭 검산하기!!! 잊지 맙시다.
그리고 현장에 따라 같은 운송경로 최적화라도 최적화 문제를 푸는 과정이 다르니 주의합시다!
다음부터 이어질 [파이썬 데이터 분석 #8장]의 내용은 더 재밌습니다.
바로 '파이썬을 활용한 시뮬레이션'을 해볼 것입니다.
이번에는 소비자의 데이터를 가지고 와서, 소비자 입소문을 통해 어떻게 입소문이 전파되는지, 회원이 증가 or 이탈하는지를 예측하는 용도로 시뮬레이션을 해봅니다. 긴 포스팅 읽어주신 분들 감사드립니다! :)
'Data Science > Analysis Study' 카테고리의 다른 글
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (2) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.03 |
|---|---|
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (1) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.02 |
| 파이썬 생산계획 최적화 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (2) | 2022.04.29 |
| 파이썬 운송 최적화 -2편 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (2) | 2022.04.28 |
| 파이썬 운송 최적화 -1편 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.04.27 |




