Yours Ever, Data Chronicles
파이썬 운송 최적화 -1편 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 본문
파이썬 운송 최적화 -1편 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100
Everly. 2022. 4. 27. 23:00안녕하세요 Everly입니다. 이번 포스팅부터는 [파이썬 데이터 분석 #7장]을 리뷰해봅니다.
지난 포스팅에선 새로운 데이터로 운송비용 최적화를 시도했지만, 실패했었죠?
이번에는 파이썬의 최적화 라이브러리를 활용하여 다시 도전해봅시다! :)
여기서 활용할 라이브러리는 python pulp, ortoolpy 라이브러리입니다.
- pulp: 최적화 모델 작성 라이브러리
- ortoolpy: 목적 함수 생성 라이브러리
먼저, 테크닉을 시작하기 전에 두 개의 라이브러리를 설치해줍니다. 아나콘다 프롬프트를 열어 다음을 입력합니다.
pip install pulp
pip install ortoolpy
저는 이 패키지들을 설치하는 과정에서 여러 에러가 떠서 애를 먹었었는데요ㅠ.ㅠ 대다수는 에러 없이 잘 설치될 것입니다.
저의 경우엔 pip upgrade를 하라는 에러 메세지가 계속 나왔는데, 그렇다고 업그레이드 코드를 치면 또 빨간 글씨로 에러가 엄청 나오더라구요(무섭...) 저와 같은 에러가 나는 분들을 위해, 이를 해결하는 포스팅(클릭)을 작성해두었으니 참고하세요 :)
✔Table of Contents
Tech 61. 운송 최적화 문제 풀기(pulp, ortoolpy 라이브러리 활용)
import numpy as np
import pandas as pd
from itertools import product
from pulp import LpVariable, lpSum, value
from ortoolpy import model_min, addvars, addvals
#데이터 불러오기
df_tc = pd.read_csv('7장/trans_cost.csv', index_col = '공장') #W-F 이동 시 발생하는 운송비용 -> 앞으로 이걸 최소화하는 게 목적
df_demand = pd.read_csv('7장/demand.csv') #공장(F)의 최소한의 필요 수요량
df_supply = pd.read_csv('7장/supply.csv') #창고(W)의 최대 가능 공급량
display(df_tc, df_demand, df_supply)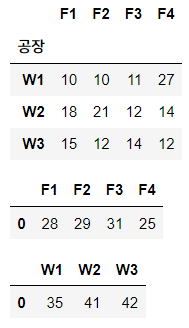
이제 필요한 라이브러리를 import하고, 최적화에 사용할 데이터를 불러옵니다.
이번 장에서도 저번 6장과 마찬가지로, 창고(W)에서 공장(F)으로 가는 경로를 최적화하는데, 목적은 '운송 비용을 최소화'하는 것이었습니다. 기억나시죠?
df_tc 라는 데이터는 W에서 F로 가는 데 발생하는 비용이며, df_demand와 df_supply는 각각 F의 최소수요량, W의 최대공급량입니다. 이 두개 데이터셋은 운송 비용을 최소화하는 데 적용되는 제약 조건이겠죠?
pulp, ortoolpy 두 개의 라이브러리를 사용하는 순서는 이렇습니다.
1) 먼저, 수리 모델 작성! 목적함수 m1을 정의하고(목적: 비용 최소화), 제약 조건을 추가해줍니다.
여기서 말하는 제약 조건은 최소 수요량 이상, 최대 생산량 이하를 만족하는 것이겠죠!
2) 다음으로는 최적해(optimal solution)인 v1을 만듭니다. 이는 비용을 최소화시킬 때의 해로, 최적의 운송 경로(운송량)를 의미합니다. 창고에서 공장으로 가는 데 몇 개의 운송량을 배분하면 최적이 되는지를 구합니다.
이는 pulp 라이브러리의 value 함수를 사용하면 됩니다.
3) 마지막으로 최적값(optimal value)을 구합니다. 이는 최소화된 운송 비용을 의미합니다. 마찬가지로 value 함수를 사용합니다.
참고로 최적해, 최적값 이런 용어가 헷갈리시는 분들은 제가 포스팅한 [최적화 문제란?] 을 참고하세요!
그럼 이제 시작해볼까요?
#초기 설정
np.random.seed(1)
nw = len(df_tc.index) #W 창고 개수 : 3
nf = len(df_tc.columns) #F 공장 개수 :4
pr = list(product(range(nw), range(nf))) #product 함수는 W(0~2)와 F (0~3)넘버를 중복 없이 짝지어줌
print(pr)
'pr' 변수에 W와 F 넘버를 중복 없이 튜플 형태로 짝짓습니다.
#수리 모델 작성
m1 = model_min() #목적 함수. 현재 초기화됨. -> 목적은 최소화! (이후 제약조건을 추가할 것임)
v1 = {(i, j) : LpVariable('v%d_%d'%(i, j), lowBound=0) for i, j in pr}
print(m1)
print(v1)
다음으로는 1번. 기본적인 수리모델을 만듭니다.
우리의 목적 함수는 m1이고, 최적해는 v1입니다.
지금은 아무런 조건도 넣지 않은 상태입니다. m1은 최소화를 목표로 하고 있으며, variable은 아무것도 없는 상태(None)입니다.
최적해를 구하기 위해선 pulp 라이브러리의 LpVariable 함수를 사용합니다.
이 함수의 인자는 lowBound, upBound가 있는데, 각각 하한선과 상한선을 의미합니다.
최적해는 최적 운송량을 뜻한다고 했죠? 당연히 0 이상이어야 합니다. 그래서 하한선을 0으로 설정했습니다.
지금은 v1의 값이 v0_0 ~ v2_3 까지 외계어로 되어 있지만, 최적화를 마치고 나면 여기에 값이 들어가게 됩니다.
#목적함수(m1)에 제약조건 추가하기
m1 += lpSum(df_tc.iloc[i][j] * v1[i,j] for i, j in pr) #목적함수 계산: 아깐 None 이었는데 값이 추가되었다.
## 창고(W) - 창고별 총 공급량 <= 창고가 공급할 수 있는 최대량
for i in range(nw):
m1 += lpSum(v1[i,j] for j in range(nf)) <= df_supply.iloc[0][i]
## 공장(F)- 공장별 총 수요량 >= 공장에서 필요로 하는 최소수요
for j in range(nf):
m1 += lpSum(v1[i,j] for i in range(nw)) >= df_demand.iloc[0][j]
m1.solve() #최적해 구해줘!
이제 목적함수 m1에 제약조건을 추가합니다. 이 제약조건은 앞서 말했듯 수요와 공급을 바탕으로 짜면 되겠죠.
이 원리를 도식화하면 다음과 같습니다. (이해를 돕기 위해, 최적해 값이 계산된 v1 값을 사용했습니다)
자세한 설명은 6장에서 이미 했으므로 넘어갑니다.


# 결과
print(m1)
결과를 뽑아보면 또 약간 외계어(?) 같지만, 다시 찬찬히 봐봅시다.
10*v0_0 + 10*v0_1 + 11*v0_2 + 27*v0_3 + 18*v1_0 + 21*v1_1 + 12*v1_2 + 14*v1_3 + 15*v2_0 + 12*v2_1 + 14*v2_2 + 12*v2_3 + 0
먼저 이 부분은 목적 함수의 계산값입니다. 목적함수는 총 운송비용이기 때문에, 창고-> 공장으로 가는 총 운송량*각 비용을 곱한 값의 합이죠.
SUBJECT TO
_C1: v0_0 + v0_1 + v0_2 + v0_3 <= 35
_C2: v1_0 + v1_1 + v1_2 + v1_3 <= 41
_C3: v2_0 + v2_1 + v2_2 + v2_3 <= 42
_C4: v0_0 + v1_0 + v2_0 >= 28
_C5: v0_1 + v1_1 + v2_1 >= 29
_C6: v0_2 + v1_2 + v2_2 >= 31
_C7: v0_3 + v1_3 + v2_3 >= 25
이 부분은 뭔가요? 그렇죠! 바로 제약 조건입니다.
C1~C3는 각 창고별 공급량이 최대공급량 안쪽으로 있을 조건이며, C4~C7은 각 공장별 수요량이 최소수요량 이상을 만족할 조건입니다.
바로 이렇게 목적함수 m1이 만들어졌고, 제약조건도 잘 들어갔네요!
이제는 pulp 라이브러리의 value 함수를 활용해 우리가 너무 구하고 싶은!! 최적값과 최적해를 구해봅니다.
# 최적해, 최적값 계산 #
df_tr_sol = df_tc.copy()
total_cost = 0
for k,x in v1.items():
i,j = k[0],k[1]
df_tr_sol.iloc[i][j] = value(x) #구해진 최적해 (v1)
total_cost += df_tc.iloc[i][j]*value(x) #최적화 이후 총 비용값 (이는 원래비용 * 최적해(v1) = 최적값 )
display(df_tr_sol) #최적해
print("총 운송 비용(최적값):", total_cost) #총 운송비용 (최적값)
당연한 말이지만 여기서 value 함수는 딕셔너리의 value가 아니라, pulp 라이브러리의 value 함수입니다.
이 함수를 활용하면 최적값과 최적해 둘을 모두 구할 수 있습니다.
먼저 최적해(여기선 v1 변수에 담김)를 살펴보죠.
최적해는 운송비용을 최소로 만드는 운송량을 뜻한다고 했죠? 이 최적해를 담을 데이터프레임을 df_tc값을 복사한 df_tr_sol 로 만들어줍니다.
v1은 앞에서도 봤지만 딕셔너리 형태로 되어 있습니다. v1.items() 로 k와 x값을 뽑아보면 key와 value 값이 나옵니다.
예를 들어 v1의 첫 번째 값은 (0,0): v0_0 이었죠.
즉, 여기서 가리키는 k는 (0,0) 이고 x는 v0_0입니다. 우리는 x값에 pulp의 value 함수를 씌우면 최적해를 구할 수 있습니다. 그래서 구해진 것이 df_tr_sol 이죠.
또한 최적값은 각 운송비용(df_tc 값)에 최적이 운송량(df_tr_sol) 을 곱해서 만들어집니다. 여기선 total_cost 라는 변수에 최적값을 담았습니다.
value(m1.objective) #최적값 (optimal value)
(참고) 한가지 팁은, 위처럼 최적값을 구할 필요 없이 위의 코드를 실행하면 바로 나옵니다.
코드로만 이해하기엔 살짝 복잡하죠? (제가 이걸 쓰고 있는데도 좀 복잡하네요,,ㅎㅎ) 이해가 안 되시는 분들은 다음 사진을 봐주세요!
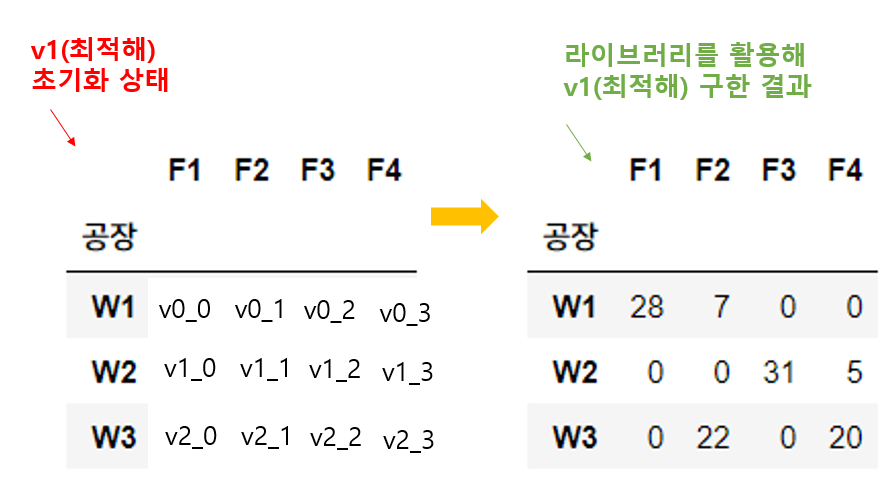
바로 이러한 원리로 초기화된 vi_j 값이 최적화 라이브러리를 활용해 구해진 값으로 채워졌다는 것입니다.

그리고 우리가 구한 최적값(optimal value)은 "총 운송 비용" 이었는데,
바로 df_tc 운송비용 값과, v1 운송량 값을 일대일 대응시켜 곱한 합이 최적값이 됩니다. 직접 일일이 계산기로 계산해보니, 정확하게 1296이 나오네요!
후후 힘들게 달려왔습니다. 총 운송비용은 1296만원으로, 6장에서 계산한 총 운송비용이었던 1433만원보다 더 비용이 절감되었네요. 최적값을 잘 구한 것 같네요!
또한 최적해(v1) 값을 보아하니, W에서 F로 가는 특정 경로에 몰빵하도록 운송량을 배치하는 것이 비용을 최소화시키는 것 같습니다.
오늘 포스팅이 생각보다 길어진 관계로, 여기서 마무리하고 '운송 최적화' 2편은 다음 포스팅으로 이어집니다!
'Data Science > Analysis Study' 카테고리의 다른 글
| 파이썬 생산계획 최적화 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (2) | 2022.04.29 |
|---|---|
| 파이썬 운송 최적화 -2편 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (2) | 2022.04.28 |
| 물류 이동 경로 최적화하기 (python optimization, 목적함수, 제약조건) / 파이썬 데이터 분석 실무 테크닉 100 (4) | 2022.04.17 |
| 파이썬 네트워크 시각화 분석하기(python networkx 예제) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.04.16 |
| 최적화 문제란? (python optimization) / 파이썬 데이터 분석 실무 테크닉 100 (1) | 2022.04.16 |




