Yours Ever, Data Chronicles
최적화 문제란? (python optimization) / 파이썬 데이터 분석 실무 테크닉 100 본문
최적화 문제란? (python optimization) / 파이썬 데이터 분석 실무 테크닉 100
Everly. 2022. 4. 16. 17:45안녕하세요, Everly입니다!
오늘부터 포스팅될 [파이썬 데이터 분석 #6장, #7장] 에서는 물류 데이터를 활용한 최적화 문제를 푸는 과정을 리뷰해보려고 합니다.
그리고 '데이터 분석 실무 테크닉 100' 책이 Tech 100까지로 이루어져 있는데, 저번 포스팅에서 벌써 Tech 50까지 왔더라구요! 이제 남은 50가지 테크닉도 잘 포스팅해보도록 할게요 :)
✔Table of Contents
최적화 문제란?
이번 포스팅부터 진행할 최적화 문제는 앞서 풀어봤던 머신러닝 문제(파이썬 데이터 분석 #4, 5장)보다도 좀 더 어렵습니다.
우선 최적화가 무엇이고, 어떤 경우에 최적화 문제를 사용하는지에 관해 알아보겠습니다.
책에서 살펴볼 최적화 문제는 '물류 데이터'를 활용합니다.
당신은 지금 어떤 기업의 창고에 있습니다. 그 창고에는 1만 개의 상품 재고가 보관되어 있습니다.
상품은 전국 대리점에서 판매됩니다. 이 기업이 갖고 있는 창고는 지금 당신이 있는 창고뿐만이 아닙니다. 전국에 흩어져 있습니다.
더 복잡한 것은 전국 여러 공장에서 생산된 상품이 각각의 창고에 도착한다는 사실입니다.

우리는 이렇게 복잡한 물류 데이터를 활용하여, 물류 기업에게 컨설팅을 해 줄 것입니다. 예를 들면 이런 것이 있겠죠?
- 어떤 물품을 얼마나 생산하는 것이 효율적인가?
- 어느 창고에 얼마만큼의 재고를 보관하는 것이 효율적인가?
- 어느 창고에서 대리점까지 몇 개의 상품을 운송하는 것이 효율적인가?
등등 정말 많은 문제가 있을 것입니다. 이렇게 가장 효율적인 생산 계획을 만드는 것, 가장 효율적인 운송 경로를 계획하는 것을 '최적화(Optimization)' 방법을 통해 해낼 수 있습니다.
책에 나온 최적화의 구체적인 정의는 다음과 같습니다.
최적화 문제란 정해진 제약조건(constraint) 아래 목적함수(Objective function)를 최소화(또는 최대화)하는 문제입니다.
예를 들어 물류 데이터의 경우, '운송 최적화'는 운송 비용을 최소화하는 것, '생산 계획 최적화'는 이익을 최대화하는 문제로 볼 수 있습니다.
이런 최적화 문제를 푸는 방법은 변수의 값이나 조합을 바꿔가면서 목적함수를 최소화(또는 최대화)시키는 지점을 찾는 것입니다.
- 목적함수를 최소화(또는 최대화)시키는 바로 그 지점을 최적해(optimal solution) 라고 합니다.
- 그리고 그 최적해 값을 가질 때 목적함수의 값을 최적값(optimal value) 라고 합니다.
혹시 경사하강법(Gradient descent)을 아시나요? 회귀 문제를 푸는 알고리즘 중에 하나로 경사하강법을 사용하기도 하는데, 회귀분석을 공부해보셨다면 회귀분석에서 coefficient 값을 찾을 때 경사하강법을 사용하는 것을 아실 것입니다.(다른 말로는 '최소제곱법' 이라고도 합니다.)
이 때 우리는 '잔차제곱합(RSS)을 최소화하는 회귀 계수를 찾는 것'에 바로 그 목적이 있었죠. 이 또한 최적화에 속합니다.

바로 위의 그림처럼 경사하강법은 Loss function을 최소화하는 지점(미분 시 0이 되는 지점)을 찾고 그 때의 값이 weight(가중치)가 되죠.
→ 이를 회귀분석에 적용한다면 RSS(잔차제곱합)을 최소화하는 지점을 찾고 그 때의 값이 coefficient(회귀계수)가 되는 것과 같습니다.

→ 마찬가지로 최적화 문제에서는 목적함수(objective function)을 최소화(or 최대화)하는 지점을 찾고 그 때의 값이 최적해(optimal solution) 라고 할 수 있습니다.
실무에서 만날 수 있는 최적화 문제
앞선 장에서 살펴본 머신러닝과 마찬가지로, 최적화도 잘 활용될 수 있는 분야가 있고 아닌 분야가 있습니다.
머신러닝의 경우 고객의 이용횟수나 이탈을 예측하는 등, B2C 기업의 실무를 할 때 잘 맞습니다. (커머스 업계, 게임 업계, 콘텐츠 업계 등 유저를 분석하는 일)
최적화는 시간이나 경로를 계산하는 분야에서 빛을 발합니다. 이를테면 지하철에서 운행 스케줄을 계획하는 것, 물류창고에서 대리점까지의 최적 경로를 탐색하는 것, 모빌리티 업계에서 차량을 재배치하는 방법을 구할 때 최적화 문제를 활용하면 좋습니다.
이는 대표적인 최적화가 활용되는 예시이고, 그 외에도 '더 효율적으로 작업하고 싶다'라고 느끼는 부분이 있다면 얼마든지 최적화 문제를 적용할 수 있습니다. 책에서는 인사관리 목적으로 아르바이트 타임스케줄을 짠다거나, 편의점에서 손님 동선을 파악한 후 상품의 진열을 하는 데에도 최적화를 적용할 수 있다고도 하네요! :)
이런 최적화 문제를 풀기 위해선 우선 목적 함수(objective function)와 제약조건(constraint)을 정의하는 것이 필요합니다. 또한 가장 최적의 값을 찾기 위해선 여러 변수를 일일이 조정하면서 맞춰보는 방법도 있지만, 파이썬 라이브러리를 활용하거나 유명한 최적화 문제의 경우 어떻게 구하는지 연구가 되어 있는 것들이 있으므로 이를 참고해서 해결할 수 있습니다.
최적화 문제에는 크게 선형 최적화, 비선형 최적화, 조합 최적화라는 3가지 패턴으로 나눌 수 있는데, 여기서는 비교적 간단한 모델인 선형 최적화에 대해서 다룹니다.
사실 저는 최적화 문제를 다뤄보는 것은 실무나 프로젝트에서 경험해본 적이 없어서, 이번에 처음 해보는 것이었는데요! 처음엔 어렵게 느껴지기도 했지만 경사하강법과 비슷한 원리라 수월하게 따라갈 수 있었던 것 같습니다. 이 책을 공부하고 공부한 걸 공유하면서 많이 배우는 것 같아요. 이번 최적화 포스팅도 많은 분들께 도움이 되기를 바랍니다.
p.s. 참고로, 통계학 전공 시간에 라그랑주 승수법(Lagrange Multiplier Method)을 배운 적이 있는데, 다시 살펴보니 라그랑주 승수법이 최적화와 같은 원리더라구요. 이 방법은 경제학이나 산업공학에서도 배운다고 하던데, 공부하신 적 있는 분들이라면 최적화 문제도 쉽게 해보실 수 있을 거 같아요 :)
이번 포스팅에서는 물류 데이터를 살펴보고 마무리하도록 하겠습니다. 먼저 컨설팅을 요청한 업체의 요청사항을 들어볼까요?
[고객의 소리] 우리 회사는 제품의 제조에서 물류까지 도맡아서 하고 있습니다. 최근 데이터 분석이라는 것을 알게 되어 상담을 받아 보려고 합니다.
최근 회사 이익이 감소하고 있어서 물류비용을 줄이고 효율화를 생각하고 있습니다. 먼저, 제품의 부품을 보관하는 창고에서 생산 공장까지 운송 비용을 낮출 수 있을지 검토하고 싶습니다. 분석을 부탁드립니다.
여기서 사용하는 데이터는 2019년 1월 1일부터 2019년 12월 31일까지의 데이터입니다.
- tbl_factory.csv : 공장 데이터 (fac)
- tbl_warehouse.csv : 창고 데이터 (w)
- rel_cost.csv : 창고 - 공장 간 운송비용 (cost)
- tbl_transaction.csv : 2019년 공장으로의 부품 운송실적 (trans)
Tech 51. 물류 데이터를 불러오자
import pandas as pd
fac = pd.read_csv('6장/tbl_factory.csv', index_col = 0)
w = pd.read_csv('6장/tbl_warehouse.csv', index_col = 0)
cost = pd.read_csv('6장/rel_cost.csv', index_col = 0)
trans = pd.read_csv('6장/tbl_transaction.csv', index_col = 0)
print(fac.shape, w.shape, cost.shape, trans.shape)
display(fac.head(), w.head(), cost.head(), trans.head())

데이터를 보면, 모든 4개의 데이터에 공통으로 존재하는 것은 '공장 정보'와 '창고 정보'임을 알 수 있습니다.
그래서 이 2개 컬럼을 key로 하여 데이터를 조인하겠습니다. (단, fac, w, cost에서의 컬럼명은 각각 FCID, WHID지만 trans 데이터에서만 ToFC, FromWH로 컬럼명이 다르므로 주의! 이름만 다를 뿐 동일한 값임)
가장 중요한 테이블은 운송실적(trans) 이므로 이 데이터를 중심으로 각 정보를 left join하겠습니다.
#먼저, trans에 cost 조인
join_data = pd.merge(trans, cost, left_on = ['ToFC', 'FromWH'], right_on = ['FCID', 'WHID'], how= 'left')
#그다음은 공장정보(fac) 조인
join_data = pd.merge(join_data, fac , on = 'FCID', how='left')
#그다음은 창고정보(w) 조인
join_data = pd.merge(join_data, w, on = 'WHID', how='left')
#이제 직관적으로 보기 쉽게 컬럼 순서 지정
join_data = join_data[['TransactionDate', 'Quantity', 'Cost', 'ToFC', 'FCName', 'FCDemand', 'FromWH', 'WHName', 'WHSupply', 'WHRegion']]
join_data.head()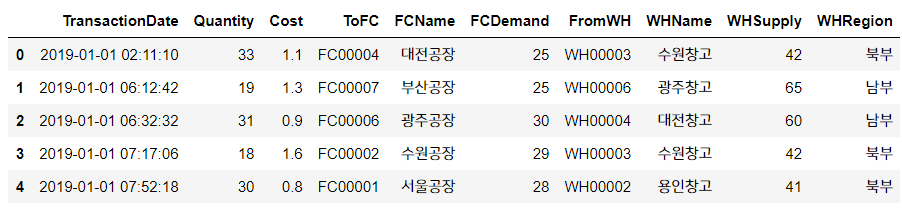
다음으로는 Region이 북부/남부인 것으로 나누어 저장합니다.
#이제 Region이 북부/남부인 것으로만 나누어 저장
north = join_data.loc[join_data['WHRegion'] == '북부']
south = join_data.loc[join_data['WHRegion'] == '남부']
print(len(north), len(south))
Tech 52. 현재 운송량과 비용을 확인하자.
이제 데이터가 잘 불러와졌습니다. 북부지사와 남부지사 간에 운송량과 비용은 어떻게 되는지를 살펴보고, 효율적으로 운송이 진행되고 있는지를 간단하게 알아봅시다.
먼저 지사 간 비용과 운송량을 확인합니다.
#지사 간 비용 확인
print("북부지사 총비용: " + str(north['Cost'].sum()) + "만원")
print("남부지사 총비용: " + str(south['Cost'].sum()) + "만원")
#지사 간 운송량 확인
print("북부지사 총부품 운송개수: " + str(north['Quantity'].sum()) + "개")
print("남부지사 총부품 운송개수: " + str(south['Quantity'].sum()) + "개")
결과를 보니,
총 비용은 북부지사 > 남부지사인데,
총 운송량은 북부지사 < 남부지사로 나타나네요.
총 비용과 운송량만 봤을 때는 남부지사가 좀 더 효율적으로 운송을 하고 있는 것 같습니다. 그럼 물품 1개 당 운송비용을 계산해봅시다.
tmp = (north['Cost'].sum()/ north['Quantity'].sum()) *10000
tmp2 = (south['Cost'].sum()/ south['Quantity'].sum()) *10000
print('북부지사 부품 1개당 운송비용: ' +str(int(tmp)) + '원') #소수점으로 나오는 것 방지를 위해 int로 바꿔줌
print('북부지사 부품 1개당 운송비용: ' +str(int(tmp2)) + '원')
비용의 단위는 만원이기 때문에 tmp, tmp2를 구할 때 뒤에 10000을 곱해주었습니다. 결과를 보니 역시 북부지사보다 남부지사의 부품 1개당 운송비용이 더 적게 드네요.
운송비용은 창고 -> 공장 간에 발생하기 때문에, 단순히 운송비용을 절감하는 것만으로도 전체 물류 비용을 억제할 수 있습니다. 이 물류 데이터를 통해 최적의 운송 경로를 만드는 것이 목적이므로 비용을 최소화해야 합니다.
마지막으로 지사 간 평균 운송비용을 확인해보겠습니다. 앞서 만든 north, south 데이터는 운영실적(trans 데이터)이 있는 것에 대해서만 걸러졌으므로 운송된 적이 없을 때의 데이터는 없었습니다. 그러므로 비용 데이터를 다시 만듭니다.
#지사 간 평균 운송비용 확인
cost_chk = pd.merge(cost, fac, on = 'FCID', how= 'left')
cost_chk.head()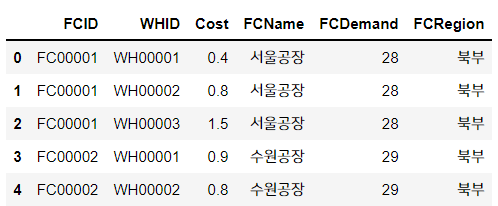
#북부/ 남부별로 평균비용값 확인
print('북부 평균비용: ', cost_chk.loc[(cost_chk['FCRegion'] == '북부')]['Cost'].mean())
print('남부 평균비용: ', cost_chk.loc[(cost_chk['FCRegion'] == '남부')]['Cost'].mean())
이상하게도 북부지역과 남부지역의 평균 비용은 거의 같습니다.
즉, 드는 비용은 동일한데, 앞서 실제 운영된 데이터로 봤을 땐 북부지역이 비용은 더 많이 쓰는데 총 운송량은 더 적었으므로 남부지역이 더 효율적으로 운송을 하고 있었다는 것을 알 수 있습니다. 뭔가 개선이 필요해 보이죠?
다음 포스팅에서는 이렇게 숫자로 알아볼뿐만 아니라, 실제로 networkx 라이브러리를 활용한 시각화를 통해 물류 최적 경로를 분석하고 컨설팅해보겠습니다. 다음 포스팅으로 이어집니다 :)
'Data Science > Analysis Study' 카테고리의 다른 글
| 물류 이동 경로 최적화하기 (python optimization, 목적함수, 제약조건) / 파이썬 데이터 분석 실무 테크닉 100 (4) | 2022.04.17 |
|---|---|
| 파이썬 네트워크 시각화 분석하기(python networkx 예제) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.04.16 |
| 머신러닝을 활용한 고객 이탈 예측 - 모델링 / 파이썬 데이터 분석 실무 테크닉 100 (4) | 2022.04.13 |
| 머신러닝을 활용한 고객 이탈 예측 - 전처리 / 파이썬 데이터 분석 실무 테크닉 100 (6) | 2022.04.12 |
| 머신러닝을 활용한 고객 이용 횟수 예측 - 모델링 / 파이썬 데이터 분석 실무 테크닉 100 (6) | 2022.04.06 |




