이렇게 모델링을 위한 데이터 가공을 마쳤습니다. 이제는 모델링을 직접 해봅시다.
✔Table of Contents
Tech 38. 선형회귀 모델링
모델 구축에 앞서, pred_data 전처리를 한번 더 합니다.
가입일자(start_date) 변수가 2018년 4월 이후인 데이터로만 데이터를 한정합니다. 왜냐하면 만들어둔 이용횟수 변수의 날짜가 모두 2018년 4월~2019년 3월이거든요. 너무 오래 전부터 있던 회원은 가입시기 데이터가 존재하지 않거나 이용횟수가 안정적일 가능성이 높기 때문에 비교적 신규인 회원들로만 데이터를 다시 만들어봅니다.
print(pred_data.shape)
pred_data = pred_data.loc[pred_data['start_date'] >= pd.to_datetime('20180401')]
pred_data.reset_index(inplace=True, drop=True) #인덱스 삭제
print(pred_data.shape)
원래 데이터가 15113개였는데, 전처리 후엔 1702개로 굉장히 많이 줄어들었네요.
여기서 사용할 모델은 가장 기본적인 '선형 회귀(Linear Regression)' 입니다. 사이킷런의 라이브러리를 이용합니다.
#선형회귀 모델 적용
from sklearn import linear_model as lm
import sklearn.model_selection
model = lm.LinearRegression()#학습할 독립변수
X = pred_data[['cnt_0', 'cnt_1', 'cnt_2', 'cnt_3', 'cnt_4', 'cnt_5', 'period']]
#학습할 종속변수
y = pred_data['cnt_pred']
#학습: 먼저 train/ test set으로 나눔 (여기서 test set은 validation set을 의미함- 모두 학습에 사용할 거니까)
## 디폴트로는 train: test 75%: 25% 로 분할됨
X_train, X_test, y_train, y_test = sklearn.model_selection.train_test_split(X, y)
model.fit(X_train, y_train)
train data(학습 데이터)인 'pred_data'를 갖고 모델을 만듭니다.
주의할 점은, 성능 검증을 위해 이 train data를 분할해야 한다는 것입니다. 여기서는 아무런 옵션을 쓰지 않고 디폴트로 분할했기에 train / test셋이 75: 25 정도로 분할되었습니다.
그리고 사이킷런에서 분할하는 메서드는 train_test_split인데, 이건 train data를 분할한 것이므로 train set, validation set을 만든 것입니다. (test 셋은 아직 만들지 않았기에 존재하지 않습니다. 이름이 헷갈릴 수 있어 주의!)
#검증
print(model.score(X_train, y_train))
print(model.score(X_test, y_test))
결과를 살펴보면 기본적인 모델이라 그런지, 정확도가 크지 않습니다.
train set에 대해서는 61%, validation set에 대해서는 57%의 정확도를 보입니다. 정확도가 약 60% 정도의 모델이네요.
모델을 바꾸거나, 변수를 바꾸거나, split 비율을 바꾸는 등의 변화를 주면 정확도가 바뀔 수 있습니다.
책에서는 이렇게 설명합니다. "정확도가 높은 예측 모델을 만들었다 할지라도, 이 모델에 대해 제대로 이해하지 못하면 현장에서 도입할 때 설명할 수가 없다."
그래서 정확도가 높은 블랙박스 모델보다는, 정확도가 낮아도 설명이 가능한 모델이 사용되는 경우가 많다고 합니다. 그래서 이런 선형 회귀 모델도 간단하기 때문에 굉장히 자주 쓰이는 모델입니다.
Tech 39. 모델에 기여하는 변수 확인하기
다음으로는 모델에 가장 크게 기여하는 변수가 무엇인지를 알아봅시다. 앞서 만든 변수 'model'에 coef_ 라는 메서드를 통해 독립변수별 기여도를 출력할 수 있습니다.
coef = pd.DataFrame({'feature_names': X.columns, 'coefficient': model.coef_})
coef
교재엔 없지만, 더 가독성을 높이기 위해 이를 시각화해보았습니다.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.barplot('feature_names', 'coefficient', data=coef)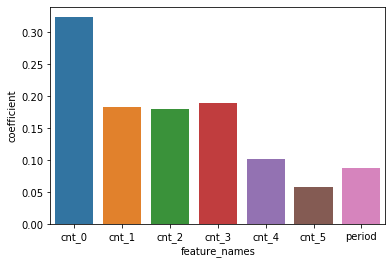
결과를 보니, cnt_0가 가장 영향력이 크며, cnt_0에서 cnt_5로 갈수록(즉, 과거 데이터로 갈수록) 기여도가 낮아짐을 확인할 수 있습니다.
즉, 바로 직전 달의 이용횟수(cnt_0)가 다음달 이용횟수(cnt_pred)에 가장 큰 영향을 미치는군요! 직감적으로도 이해가 가능한 이야기입니다.
Tech 40. 다음 달의 이용횟수를 예측하자 (나만의 방법)
마지막으로는 직접 test data에 대해 예측을 해봐야겠죠?
책에서는 정말 간단한 데이터를 임의로 만들어 예측을 합니다. 임의의 회원 2명의 이용데이터가 주어졌을 때 예측합니다.
#임의로 회원 2명의 이용데이터를 input으로 넣었을 때의 이용 횟수를 예측해보자.
x1 = [3, 4, 4, 6, 8, 7, 8]
x2 = [2, 2, 3, 3, 4, 6, 8]
x_pred = [x1, x2]
#x_pred에 대해 모델을 적용해 예측해보면?
model.predict(x_pred)
즉, 회원 1은 다음 달 약 3.9회, 회원 2는 약 1.98회를 이용할 것이라고 예측되었습니다.
여기서 더 나아가서, 교재엔 없지만 2019년 4월의 이용 횟수를 예측해보았습니다.
먼저 과거 데이터부터 만들어야겠죠? 2019년 4월의 과거 6개월 데이터는 2019년 3월 ~ 2018년 10월의 데이터가 될 것입니다. 우선은 2019년 3월의 데이터를 담은 'cnt_0' 변수를 만들어봅니다.
i =12
j = 1
tmp = ul_m.loc[ul_m['연월'] == year_months[i-j]]
del tmp['연월']
tmp.rename(columns = {'cnt': 'cnt_{}'.format(j-1)}, inplace=True)
tmp.reset_index(inplace=True, drop=True)
tmp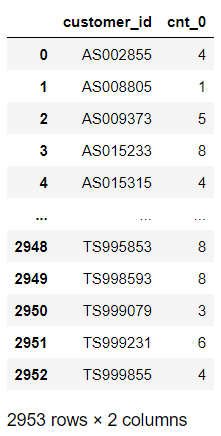
cnt_0가 만들어졌으니, 이제는 과거의 데이터 cnt_1 ~ cnt_5까지를 만들어 위 데이터에 column-bind로 붙여봅니다.
customer_id를 기준으로 조인시키면 되겠죠?
i = 12
for j in range(2, 7):
tmp_before = ul_m.loc[ul_m['연월'] == year_months[i-j]]
del tmp_before['연월']
tmp_before.rename(columns = {'cnt': 'cnt_{}'.format(j-1)}, inplace=True)
tmp = pd.merge(tmp, tmp_before, on ='customer_id', how='left')
tmp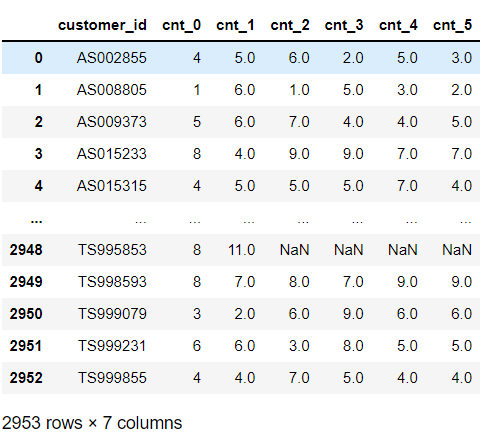
이렇게 2019년 3월 ~ 2018년 10월의 과거 데이터를 담은 'tmp' 데이터가 만들어졌습니다. (*연월을 확인하고 싶다면 del~ 이 코드를 주석처리하고 실행)
역시 전처리할 것들이 좀 보이므로 전처리를 해봅시다. 먼저 NaN을 지우고, 'c' 데이터를 조인해 가입일자를 계산해봅시다.
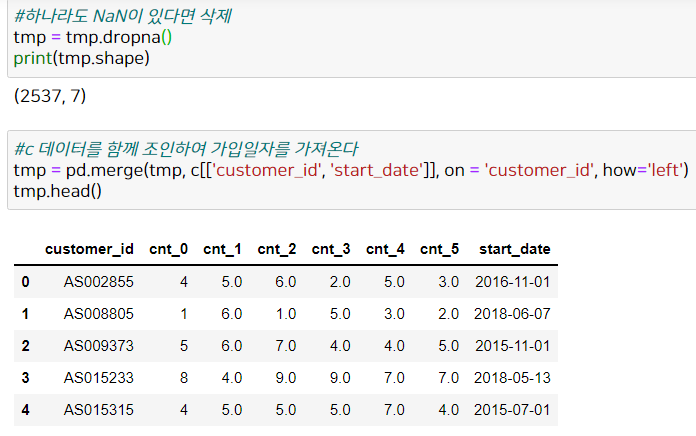
start_date(가입일자)와 연월 간 날짜 차이를 계산합니다.
그 전에 가입일자가 2018년 4월 이후인 애들만 뽑아야겠죠?
#start_date를 datetime으로
tmp['start_date'] = pd.to_datetime(tmp['start_date'])
#가입일자가 2018년 4월 이후인 애들만 뽑음 -> 399개로 줄어듦
print(tmp.shape)
tmp = tmp.loc[tmp['start_date'] >= pd.to_datetime('20180401')]
tmp.reset_index(inplace=True, drop=True) #인덱스 삭제
print(tmp.shape)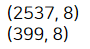
데이터가 굉장히 줄어들었네요. (2537건 -> 399건)
이제는 연월과 start_date 간 날짜 차이를 계산합니다.
이 데이터에서 '연월'은 2019년 4월을 의미합니다. 그래서 따로 2019년 4월 컬럼을 생성해 계산해줍시다.
tmp['now_date'] = pd.to_datetime('20190401')
from dateutil.relativedelta import relativedelta
tmp['period'] = None #초기화
for i in range(len(tmp)):
delta = relativedelta(tmp.loc[i, 'now_date'], tmp.loc[i, 'start_date'])
tmp.loc[i, 'period'] = delta.years*12 + delta.months
tmp.head()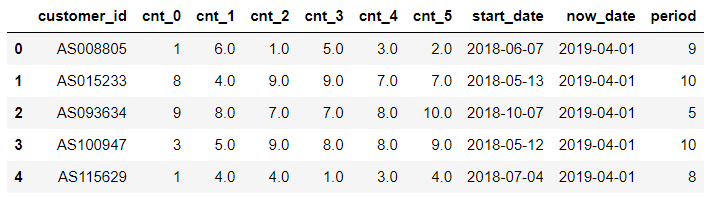
이렇게 새로운 열 'period'까지 만들어졌네요. 결측치가 있는지 확인해봅니다.
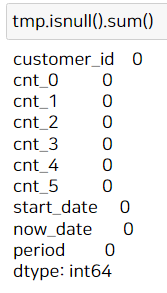
결측치가 없네요! 이제 만들어진 데이터에 대해 예측을 수행해봅니다. 이 예측 결과는 2019년 4월의 이용횟수 예측치입니다.
#이제 필요한 열만 걸러낸다.
tmp_pred = tmp[['cnt_0', 'cnt_1', 'cnt_2', 'cnt_3', 'cnt_4', 'cnt_5', 'period']]
#모델에 대해 예측한 결과는?
model.predict(tmp_pred)
결과는 399개의 값이 나옵니다.
위와 같이 2019년 4월의 예측 이용량을 계산해낼 수 있습니다. 당연한 말이지만, 2019년 4월 데이터는 주어지지 않았으므로 정답 데이터가 없기 때문에 정확도 계산은 불가능합니다. 이렇게 test data를 만들어보고, 이에 대해 예측해보았습니다.
이렇게 회원별로 과거의 데이터를 활용해, 다음 달(2019년 4월)의 이용횟수를 예측해볼 수 있습니다. 이런 예측을 바탕으로 다음 달에 다양한 정책을 실시하는 데에도 활용할 수 있겠죠?
이번 파이썬 데이터 분석 #4장에서는, Tech 35번까지는 클러스터링을 통해 회원 유형을 구분해보았고,
Tech 40번까지는 직접 선형 회귀 모델을 사용해 예측함으로써 과거의 이용이력을 바탕으로 미래의 이용이력을 예측해보았습니다.
다음 파이썬 데이터 분석 #5장에서는, 이미 탈퇴한 회원과 계속 이용하는 회원 데이터를 활용하여, Decision Tree를 사용해 탈퇴를 예측해봅니다.(즉, '고객 이탈 분석'을 해봅니다.) 고객의 행동 패턴을 분석할 수 있으면 어떤 고객이 탈퇴하는지를 예측할 수 있고, 이에 대한 방지책을 세울 수 있기에 유용한 분석이 될 것입니다.
그럼 다음 포스팅에서 만나요! 감사합니다 :)
'Data Science > Analysis Study' 카테고리의 다른 글
| 머신러닝을 활용한 고객 이탈 예측 - 모델링 / 파이썬 데이터 분석 실무 테크닉 100 (4) | 2022.04.13 |
|---|---|
| 머신러닝을 활용한 고객 이탈 예측 - 전처리 / 파이썬 데이터 분석 실무 테크닉 100 (6) | 2022.04.12 |
| 머신러닝을 활용한 고객 이용 횟수 예측 - 전처리 / 파이썬 데이터 분석 실무 테크닉 100 (4) | 2022.04.06 |
| 고객 유형을 나누기(파이썬 클러스터링, 군집 분석) / 파이썬 데이터 분석 실무 테크닉 100 (6) | 2022.04.06 |
| 파이썬 EDA : 고객의 전체 모습 파악하기 -2편 / 파이썬 데이터 분석 실무 테크닉 100 (8) | 2022.01.17 |
