Yours Ever, Data Chronicles
물류 이동 경로 최적화하기 (python optimization, 목적함수, 제약조건) / 파이썬 데이터 분석 실무 테크닉 100 본문
물류 이동 경로 최적화하기 (python optimization, 목적함수, 제약조건) / 파이썬 데이터 분석 실무 테크닉 100
Everly. 2022. 4. 17. 13:05앞선 포스팅에서 간단하게 물류 운송 데이터를 바탕으로 창고와 공장 간 이동관계를 네트워크화 해보았습니다.

결과는 위와 같았는데요! 어느 창고(W)에서 어느 공장(F)으로 가든지간에, 모든 경로가 있다는 점이 주목할 만한 점입니다. 이 중에서 굵기가 진한 엣지인 W2 → F3로 가는 경로는 운송량이 다른 경로에 비해서 더 많다는 것이 눈에 띄네요.
앞의 포스팅에서, 물류 회사에서 요청한 분석이 무엇이었는지 기억나시나요? "운송비용을 절약하기 위한 최적의 경로를 찾아달라"는 것이었죠.
그렇다면 위의 경로에서 운송비용을 더 효율적으로 만들고자 한다면 어떻게 경로가 바뀌면 될까요?
맞습니다. 직관적으로 생각해볼 수 있는 것처럼, 특정 경로에만 집중되는 것이 운송비용을 더 절약할 수 있을 것입니다.
어떤 경로만 살리고 어떤 경로는 버릴지는, ✔운송비용이 적은 경로를 선택하는 것뿐만 아니라 ✔제품의 수요와 공급에 대해서도 생각해봐야 합니다.
특정 A라는 경로가 운송비용이 적더라도, 공장에서 필요하다고 하는 수요량보다 훨씬 많이 운송을 할 필요는 없겠죠.(오히려 낭비니까요.) 또한 창고에서 최대로 생산해낼 수 있는 공급량보다 더 많이 운송을 하는 것은 불가능합니다.
이번 포스팅에서는 최적화 문제를 풀어보고, 이 물류 데이터에서 생각해볼 수 있는 최적의 경로를 간단하게 구해보겠습니다. 앞선 포스팅에서도 얘기했지만, 최적화 문제란 무엇일까요?
최적화란, 목적 함수(Objective function)를 정의하고, 제약 조건(constraint)를 정의한다. 그 후 제약 조건 하에서 해당 목적 함수를 최소화(or 최대화)할 수 있는 최적의 조건을 찾는 것이다.
그러므로 최적경로를 찾기 위해선 우선적으로 1. 목적 함수와 2. 제약조건을 찾아야 합니다. 차근차근 이 문제를 해결해보겠습니다.

✔Table of Contents
Tech 58. 운송 비용 함수(목적 함수)를 작성하자
먼저 목적 함수(objective function)를 정의해봅시다. 최적경로를 찾는 목적이 무엇이라고 했죠? 앞서 이야기했듯 "운송 비용을 낮추는 것"이 우리의 목적입니다.
그러므로 목적함수는 운송비용을 계산하는 함수가 됩니다. 먼저 운송 비용 함수부터 만들어봅시다.
이번 포스팅에서 사용하는 데이터는 다음과 같습니다.
- trans_route.csv : 운송 경로 데이터. 즉, 창고-공장 간 운송량 (df_tr)
- trans_route_pos.csv : 창고, 공장의 위치정보 (df_pos)
- trans_cost.csv : 창고-공장 간 운송비용 (df_tc)
- demand.csv : 공장에서의 제품 최소 수요량
- supply.csv : 창고가 공급할 수 있는 최대 공급량
- trans_route_new.csv : 새로 설계한 운송경로
#운송 비용을 계산하는 함수 만들기
import pandas as pd
#데이터 불러오기
df_tr = pd.read_csv('6장/trans_route.csv', index_col = '공장') #창고- 공장 간 운송 경로
df_tc = pd.read_csv('6장/trans_cost.csv', index_col = '공장') #창고-공장 간 운송하는 데 드는 비용
display(df_tr, df_tc)
이제 운송비용을 계산해봅시다. 계산은 정말 간단합니다.
어차피 창고(W) 에서 공장(F) 으로만 이동할 수 있고, df_tr에선 운송량을, df_tc에선 운송 비용이 들어있죠. 그럼 총 운송비용 = 각 경로별 운송량*운송비용의 합 으로 계산이 가능합니다. 이를 함수로 만들어봅니다.
#운송 비용 함수
def trans_cost(df_tr, df_tc):
cost = 0
for i in range(len(df_tc.index)): #i : W(창고)
for j in range(len(df_tr.columns)): #j : F(공장)
cost += df_tr.iloc[i][j]*df_tc.iloc[i][j] #운송 비용: i-> j 로 갈 때 몇 번 갔는지 * 드는 비용 을 모두 더함
return cost
#이 예제에서 총 운송비용은 얼마가 나오는지 함수를 적용해보면
trans_cost(df_tr, df_tc)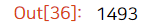
이 예제에서는 1493(만원) 의 총 운송비가 들고 있네요. 효율적인 경로를 만들어 이 운송비를 줄여봅시다!
Tech 59. 제약 조건 만들기
다음으로는 제약조건(제약식)을 만듭니다. 포스팅의 첫머리에서도 언급했지만, 제약조건은 2가지가 있었습니다.
- 창고(W): 최대 공급 가능한 부품 수가 제한되어 있음 -> supply.csv 데이터에 나온 것까지만 공급 가능. 더 많이 만들 수 없음
- 공장(F): 채워야 할 최소한의 제품 제조량이 있음 -> demand.csv 데이터에 나온 최소한의 수요량이 필요함. 더 적으면 안 됨
이를 바탕으로 제약조건 2가지를 제약식으로 만들어봅시다.
import pandas as pd
#필요한 데이터
df_tr = pd.read_csv('6장/trans_route.csv', index_col = '공장')
df_demand = pd.read_csv('6장/demand.csv')
df_supply = pd.read_csv('6장/supply.csv')
display(df_tr, df_demand, df_supply)
먼저 수요 제약조건을 만들어봅니다. 앞서 이야기했듯이, 공장에서는 최소한의 수요량이 `df_demand` 데이터에 저장되어 있습니다.
현재 운송량 데이터인 `df_tr`은 이 최소수요량을 만족하고 있는지를 코드로 확인해봅시다. df_tr 데이터의 공장별 합계(즉, 열 합계)를 구해 비교하면 되겠죠?
#수요측 제약조건
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]])
#그렇다면 temp_sum(실제 수요) >= demand(최소 수요) 여야겠지? 그 반대면 수요량을 만족시키고 있지 않을 것
if temp_sum >= df_demand.iloc[0][i]:
print('수요량 만족')
else: print('수요량 만족X. 운송경로 재계산 필요')
#정보 출력
print("공장 " + str(df_demand.columns[i]) + " 운송량: " + str(temp_sum) + " (수요량 :" + str(df_demand.iloc[0][i]) + ")" )
print(" ")
공장별 합계(df_tr의 열 합계)를 temp_sum으로 두고, 최소 수요량인 df_demand의 값과 비교합니다. temp_sum값이 더 크다면 수요량을 만족하고 있는 것이고, 아니면 수요량을 만족하지 않는 것이죠.
결과를 봤을 때 모든 공장 F1~F4가 최소수요량 이상을 만족하고 있습니다.
다음으로는 공급 제약조건입니다. 이는 반대로 창고별 합계(df_tr의 행 합계)를 temp_sum으로 두고, 최대 공급량인 df_supply보다 더 작은지를 비교하면 됩니다. 더 작다면 공급한계를 만족하고 있는 것이고, 아니면 공급한계를 초과한 것입니다.
#공급측 제약조건
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]])
#그렇다면 temp_sum(실제 공급) <= supply(최대 공급) 이어야겠지? 실제로는 최대로 공급할 수 있는 양보다 더 적거나 같을 것
if temp_sum <= df_supply.iloc[0][i]:
print('공급한계 범위내')
else: print('공급한계 초과. 운송경로 재계산 필요')
#정보 출력
print("창고 " + str(df_supply.columns[i]) + " 운송량: " + str(temp_sum) + " (공급량 :" + str(df_supply.iloc[0][i]) + ")" )
print(" ")
결과를 보면 최대 공급량도 만족하고 있습니다.
현재 운송량은 수요, 공급의 제약조건을 잘 만족하고 있습니다. 이제 새롭게 변화시킬 운송량도 이 제약조건을 꼭! 만족해야 합니다.
Tech 60. 운송 경로를 변경하고, 목적함수의 변화를 확인하자
운송비용을 줄이기 위해, W1 -> F4로의 운송을 줄이고, 대신 W2 -> F4로의 운송을 늘린 새로운 운송경로 데이터 df_tr_new 데이터를 불러오겠습니다.
과연 이렇게 운송량이 변경된다면 목적함수의 값은 어떻게 바뀔까요?
import pandas as pd
import numpy as np
#데이터 불러오기
df_tr_new = pd.read_csv('6장/trans_route_new.csv', index_col = '공장')
df_tr_new
#운송 비용 계산
print('기존:', trans_cost(df_tr, df_tc), '변경:', trans_cost(df_tr_new, df_tc))
목적함수 값만 본다면, 아까 전에는 1493만원이었는데 이제는 총 비용이 1428만원으로 많이 줄었습니다. 앗, 그럼 최적 경로를 찾은 것일까요?!
아직 수요와 공급 제약조건을 충족시키는지를 확인하지 않았습니다. 이 조건을 충족하는지를 출력하는 수요와 공급 함수 c_demand와 c_supply를 새로 만들겠습니다.
이 함수는 운송경로 데이터와 함께 수요, 공급 데이터를 input으로 받습니다.
그리고 최소 수요 이상이면 1, 아니면 0
최대 공급 이하이면 1, 아니면 0을 반환합니다.
#제약조건 함수화 -> 앞서 만든 if문에서, 수요(or 공급)을 만족하면 1, 아니면 0을 출력하도록 하는 flag를 만든다.
## 먼저 0으로 초기화시키고, 만족하는 경우엔 1을 넣어주기
## 공장(F)의 수요
def c_demand(df_tr, df_demand):
#초기화
flag = np.zeros(len(df_demand.columns))
#계산
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]])
if temp_sum >= df_demand.iloc[0][i]:
flag[i] = 1
return flag
## 창고(W)의 공급
def c_supply(df_tr, df_supply):
#초기화
flag = np.zeros(len(df_supply.columns))
#계산
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]])
if temp_sum <= df_supply.iloc[0][i]:
flag[i] = 1
return flag
이제 결과를 확인해볼까요?
#수요 계산 결과
c_demand(df_tr_new, df_demand)
새로운 데이터는, 모든 공장이 최소수요를 만족하고 있습니다.
#공급 계산 결과
c_supply(df_tr_new, df_supply)
그런데 공급에 대해선, 한 창고의 운송량이 최대공급을 넘어서는군요. 이렇게 되면 최대로 공급할 수 있는 것보다 더 많은 제품이 필요하기 때문에 이 데이터로는 최적경로를 만들 수 없습니다. 다른 운송량 데이터가 필요하겠네요.
이렇게 해서 [파이썬 데이터 분석 #6장]을 마무리합니다. 이번 6장에서는 최적화 문제의 개념과, networkx 함수를 활용한 경로 시각화 방법, 그리고 목적함수와 제약조건을 설정하는 방법을 배웠습니다. 생소한 개념이지만, 재밌지 않나요? ㅎㅎ
다음 포스팅인 [파이썬 데이터 분석 #7장]에서는 6장에서 배운 것을 더 심화하여 데이터 분석을 해봅니다.
방금 전에 새로운 운송데이터를 활용해 최적화 문제를 해결했는지를 확인했는데, 해결을 못했습니다.
이렇게 최적경로를 찾을 때에는 값을 바꿔보면서 최적값이 되는지를 확인해볼 수도 있지만, 최적화 라이브러리를 사용하면 좀 더 쉽게 최적화 문제를 해결할 수 있습니다. 7장에서는 최적화 라이브러리를 활용해 운송 최적화 문제에 다시 도전해보겠습니다.
그럼 다음 포스팅에서 만나요! :)
'Data Science > Analysis Study' 카테고리의 다른 글
| 파이썬 운송 최적화 -2편 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (2) | 2022.04.28 |
|---|---|
| 파이썬 운송 최적화 -1편 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.04.27 |
| 파이썬 네트워크 시각화 분석하기(python networkx 예제) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.04.16 |
| 최적화 문제란? (python optimization) / 파이썬 데이터 분석 실무 테크닉 100 (1) | 2022.04.16 |
| 머신러닝을 활용한 고객 이탈 예측 - 모델링 / 파이썬 데이터 분석 실무 테크닉 100 (4) | 2022.04.13 |




