Yours Ever, Data Chronicles
파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (2) / 파이썬 데이터 분석 실무 테크닉 100 본문
파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (2) / 파이썬 데이터 분석 실무 테크닉 100
Everly. 2022. 5. 3. 12:32저번 포스팅에서는 SNS 입소문을 타고 전파되는 과정을 시뮬레이션 해보았습니다.
이번 포스팅은 저번 포스팅과 이어지니 안 보신 분들은 보고 오는 걸 추천드려요!
✔Table of Contents
Tech 73. 입소문 전파를 시계열 그래프로 나타내자
이전 포스팅에서 간단한 네트워크 시각화를 통해, 입소문의 위력이 얼마나 컸는지를 알 수 있었습니다.
하지만 모든 개월수에 대해 시각화를 해서 총 36개의 이미지를 만들기엔 너무 보기가 힘들겠죠?
그래서 단 하나의 시계열 그래프로 만들어서 살펴보겠습니다. 개월별 전파수의 합을 구하고, x축을 개월, y축을 입소문 전파 수의 합으로 나타내봅시다.
먼저, 개월별 전파수 합은 어떻게 구하면 될까요? 앞에서 구한 list_ts가 각 개월별 전파현황을 리스트 내 리스트로 담고 있었죠!
그래서 예를 들어 list_ts[0]은 1개월차의 전파 현황을 담고 있습니다. 그럼 이 리스트에 sum을 하면 1개월차의 전파수 합을 볼 수 있겠군요.
print(list_ts[0], sum(list_ts[0])) #1개월차 전파수 합계
print(list_ts[9], sum(list_ts[9])) #10개월차 전파수 합계
이런 식으로 하면 아주 간단한 for문을 만들어 시계열 그래프를 그려볼 수 있습니다.
list_ts_num 이라는 새로운 리스트를 만들어, 개월별 전파수 합계를 차곡차곡 담아봅니다.
list_ts_num = []
for t in range(len(list_ts)):
list_ts_num.append(sum(list_ts[t]))
plt.plot(list_ts_num)
plt.show()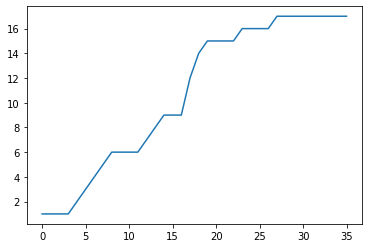
위 그래프를 통해, x축(개월수)의 값이 커질수록 전파수가 크게 늘어남을 한눈에 파악할 수 있습니다. (그리고 이전 포스팅에서도 말했듯, 실행할 때마다 다른 값이 나오므로 그래프도 달라집니다.)
Tech 74. 확산 및 소멸확률을 이용해 입소문 전파를 시뮬레이션하자
앞에서 했던 시뮬레이션은 오로지 '확산'확률만을 이용했습니다. 입소문 전파 확률을 임의로 10%로 가정하고 입소문이 전파되는 과정을 시뮬레이션해보았는데요!
하지만 현실에서는 이렇게 '전파'만 일어나는 게 아니라, 전파와 상관없이 고객이 탈퇴하는 경우도 발생하죠. 이럴 때의 '소멸' 확률을 활용해 시뮬레이션을 해보겠습니다.
앞에서 전파(확산)확률을 10%라고 임의로 설정했듯이, 탈퇴(소멸)확률은 임의로 5%로 설정하겠습니다.
확률을 설정하는 방식은 이전 포스팅에서 만든 determine_link 함수를 그대로 사용하겠습니다.
def simulate_population(num, list_active, percent_percolation, percent_disappearence, df_links):
#확산 - 이전에 만든 코드 그대로
for i in range(num):
if list_active[i] == 1:
for j in range(num):
if df_links.iloc[i][j] == 1:
if determine_link(percent_percolation) ==1:
list_active[j] = 1
#소멸
for i in range(num):
if determine_link(percent_disappearence) == 1:
#반대로 랜덤확률이 소멸할 확률보다도 작으면 전파가 꺼지는 것(0)으로 설정
list_active[i] = 0
return list_active
위와 같이 시뮬레이션 함수를 확산, 소멸확률 둘 다를 고려해 simulate_population을 만들었습니다.
저번에 만든 시뮬레이션 함수처럼, 초기화된 list_active를 넣으면 확산/소멸 과정을 랜덤하게 거쳐 바뀐 list_active가 반환됩니다.
percent_percolation은 확산확률로 0.1(10%), percent_disappearence는 소멸확률로 0.05(5%)를 임의로 지정하겠습니다.
이전엔 36개월을 지켜봤다면, 이번엔 T_NUM을 100개월로 해서 100개월 동안 확산/소멸을 거치면 전파 횟수가 어떻게 달라지는지를 확인합니다.
T_NUM = 100 #100개월 동안 어떻게 바뀔지 지켜보자.
NUM = len(df_links.index)
# list_active 초기화
list_active = np.zeros(NUM)
list_active[0] = 1
### 100개월 시뮬레이션 ###
list_ts = []
for t in range(T_NUM):
#임의로 확산할 확률 10%, 소멸할 확률 5%로 둠
list_active = simulate_population(NUM, list_active, 0.1, 0.05, df_links)
#시뮬레이션 과정 100번 반복해서 list_ts에 차곡차곡 쌓음
list_ts.append(list_active.copy())
이 코드를 실행하면 list_ts에 100개의 리스트가 들어있게 됩니다.
100개 리스트를 각각 네트워크 시각화하면 총 100개의 이미지가 나오니, 이렇게 하지 말고 Tech 73에서 한 것처럼 시계열 그래프로 만들어봅시다. 아까 만들었던 코드를 그대로 사용합니다.
#아까전에 만든 코드 그대로 사용
list_ts_num = []
for t in range(len(list_ts)):
list_ts_num.append(sum(list_ts[t]))
plt.plot(list_ts_num)
plt.show()
여기서 x축은 개월수, y축은 총 전파 횟수(최대: 20명)입니다.
신기하죠? 처음에 확산확률만 고려했을 때는 거의 20명 전체에 모두 전파가 되었는데, 소멸확률까지 함께 고려하니 100개월 때에도 20명 전체로 전파되지 못했습니다. 소멸확률은 고작 5%였는데도 위력이 크군요!
이번에는 소멸확률(탈퇴확률)을 5%에서 20%로 늘려보겠습니다.
## 아까 만든 코드 그대로 사용 ##
T_NUM = 100
NUM = len(df_links.index)
list_active = np.zeros(NUM)
list_active[0] = 1
list_ts = []
for t in range(T_NUM):
# 소멸확률만 0.05 -> 0.2로 늘림
list_active = simulate_population(NUM, list_active, 0.1, 0.2, df_links)
list_ts.append(list_active.copy())
list_ts_num = []
for t in range(len(list_ts)):
list_ts_num.append(sum(list_ts[t]))
plt.plot(list_ts_num)
plt.show()
아까 만든 코드를 그대로 복붙했습니다. 소멸확률만 0.05에서 0.2로 늘렸는데, 위에 그래프를 보시죠. 정말 대박이죠?
20개월이 채 되기도 전에 전파가 아예 사라졌습니다. 이용자가 0명이 되어버렸네요.
사실 어찌보면 당연한 결과입니다. 처음 시작을 이용자 1명에서 시작했는데, 전파확률(확산확률) 보다도 소멸확률이 더 높기 때문입니다.
Tech 75. 파라미터 간의 상관관계를 파악하자 (plt.matshow, plt.colorbar)
좀 궁금하지 않나요? 확산확률과 소멸확률에 따른 이용자 수의 관계가!
얼핏 봤을 땐 우선 확산확률 < 소멸확률이면 당연히 이용자 수는 0명이 됩니다. 그럼 확산확률 > 소멸확률이면 무조건 이용자는 처음보다 늘어날까요? 그 임계점이 되는 확률은 몇일까요?
이런 것을 일일이 확률을 바꿔가면서 넣으면 너무 시간이 오래 걸리겠죠. 확산확률과 소멸확률을 모두 0부터 1사이값으로 설정하고 확률 변화에 따라 이용자 수를 계산해봅시다!
확산확률과 소멸확률 모두 0.05씩 바꿔봅시다. (0, 0.05, 0.1, 0.15, 0.2, .... 0.95)
for i in range(20):
print(0.05*i)
확률을 바꾸는 코드는 위 코드를 실행하면 됩니다. 0부터 0.05 간격으로 0.95까지 20개를 출력해줍니다.
이 원리를 이용해서, i를 확산확률(i_p)로, 소멸확률(i_d)로 바꿔 코드를 짜봅니다.
## 주의! 코드 실행 시간 약 15분 걸림 ##
T_NUM = 100
NUM_phasediagram = 20
phasediagram = np.zeros((NUM_phasediagram, NUM_phasediagram)) #20x20 행렬
for i_p in range(NUM_phasediagram):
for i_d in range(NUM_phasediagram):
percent_percolation = 0.05 * i_p #확산확률
percent_disapparence = 0.05 * i_d #소멸확률
list_active = np.zeros(NUM)
list_active[0] = 1
## 100개월동안 시뮬레이션 진행
for t in range(T_NUM):
#이번엔 list_active값 개월별로 안담고 맨 마지막 개월것만 담음
list_active = simulate_population(NUM, list_active, percent_percolation, percent_disapparence, df_links)
phasediagram[i_p][i_d] = sum(list_active)
print(phasediagram)
위의 코드는 확산확률(i_p)를 0~0.95로 0.05씩 바꿔가고, 똑같이 소멸확률(i_d)도 0~0.95로 0.05씩 바꾸는 코드입니다.
그리고 앞에서 만들었던 입소문 전파 코드를 그대로 씁니다. 100개월 동안 전파과정을 지켜봅니다.
(* 참고로, 지금까지는 list_active의 개월별 값을 list_ts 라는 또다른 리스트에 차곡차곡 담았습니다(그래서 list_ts는 리스트 100개가 들어있었죠). 이번에는 그렇게 하지 않고, 100개월이 지났을 때의 list_active 값만 출력합니다.)
처음에 phasediagram이라는 20x20 행렬은 확산확률과 소멸확률이 들어갈 곳인데요,
만일 확산확률이 0, 소멸확률이 0인 것은 phasediagram의 (0,0) 인덱스에 값이 들어가겠죠. 이 때 100개월 뒤의 전파 총합계(100개월 뒤의 총 이용자 수)가 들어가게 됩니다. 사진을 보시면 이해가 더 쉬워요!

phasediagram을 2차원으로 표현해본다면 바로 위와 같은 그림이 될 것입니다.
실제로 print(phasediagram)을 해보면 요렇게 나옵니다.

이런 리스트가 20개가 나오는데요, 하나의 리스트씩 제가 위에 그린 그림의 한 행에 들어간다고 생각하면 됩니다.
matplotlib의 matshow, colorbar를 활용해 위의 20x20 매트리스를 그림으로 나타내봅시다.
plt.matshow(phasediagram)
plt.colorbar(shrink=0.8) #colorbar 길이 조정
plt.xlabel('disapparence(%)')
plt.ylabel('percolation(%)')
plt.xticks(np.arange(0.0, 20.0, 5), np.arange(0.0, 1.0, 0.25))
plt.yticks(np.arange(0.0, 20.0, 5), np.arange(0.0, 1.0, 0.25))
plt.tick_params(bottom=False, left=False, right=False, top=False)
plt.show()
바로 위의 그림처럼 나오게 됩니다. 숫자가 클수록(20에 가까울수록) 노란색, 숫자가 작을수록(0에 가까울수록) 남색이 됩니다.
그래프로 보니 좀 더 이해하기 쉽지 않나요? 확산확률과는 관계없이, 소멸확률의 값이 높으면 총 이용자 수는 무조건 0명이 됩니다.
설사 확산확률이 0.5 이상이라 하더라도, 소멸확률 값이 0.5 이상이면 무조건 0명이 됩니다. 즉, 확산확률이 아무리 높아도 소멸확률이 높으면 입소문은 무용지물이군요.
반대로, 소멸확률이 낮으면 어떤가요? 확산확률이 0~0.25인데 소멸확률이 0이면 100개월 후엔 20명 전원에게 전파가 되었습니다.
즉, 정리하면 다음과 같습니다.
- 소멸확률이 낮으면 확산확률이 어느정도 낮더라도 20명 전원이 이용한다.
- 반대로 소멸확률이 0.2를 넘어서면 확산확률이 높아도 이용자는 절대 20명 전원까지 전파될 수 없다.
입소문을 타고 이용자 수를 많이 확보하기 위해서는, 어떻게든 탈퇴하는 회원을 줄이도록 노력해야겠군요!
이렇게 해서 회원 20명의 SNS를 통한 입소문 전파가 어떻게 되는지를 시뮬레이션 해보았습니다.
지금까지는 회원 20명의 데이터를 갖고 시뮬레이션을 했는데, 다음 포스팅에선 실제 전체 회원 540명을 바탕으로 시뮬레이션을 해보겠습니다.
지금까지는 확산확률과 소멸확률을 그냥 임의로 10%, 5% 이렇게 지정을 했었죠? 다음 포스팅부터는 최적의 확산/소멸확률을 구해서 시뮬레이션에 활용해보겠습니다. 이를 알 수 있다면 우리가 확산/소멸확률을 몇 퍼센트(%) 정도로 유지해야 하는지를 알 수 있어 유용하겠죠?
그럼 다음 포스팅에서 뵐게요 :)
'Data Science > Analysis Study' 카테고리의 다른 글
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (4) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.05 |
|---|---|
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (3) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.04 |
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (1) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.02 |
| 물류 네트워크 최적화 설계 예제 (python logistics_network) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.04.30 |
| 파이썬 생산계획 최적화 (python pulp, ortoolpy) / 파이썬 데이터 분석 실무 테크닉 100 (2) | 2022.04.29 |




