Yours Ever, Data Chronicles
파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (3) / 파이썬 데이터 분석 실무 테크닉 100 본문
파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (3) / 파이썬 데이터 분석 실무 테크닉 100
Everly. 2022. 5. 4. 12:41저번 포스팅까지는 회원 20명 데이터로 입소문 전파 시뮬레이션을 해보았는데요!
이번 포스팅은 540명의 전체 회원 데이터를 갖고 시뮬레이션을 해보겠습니다. 데이터에 나와 있는 기업은 SNS 입소문이 아주 중요한 스포츠 센터입니다.
혹시 저번 포스팅을 안 보셨다면, 이번 포스팅 내용을 따라오기 힘들 수 있으니 꼭 보고 오시길 추천드립니다! (1편, 2편)
✔Table of Contents
Tech 76. 실제 데이터를 불러오자
mem_link = pd.read_csv('8장/links_members.csv')
mem_info = pd.read_csv('8장/info_members.csv')
print(mem_link.shape, mem_info.shape)
display(mem_link.head(), mem_info.head())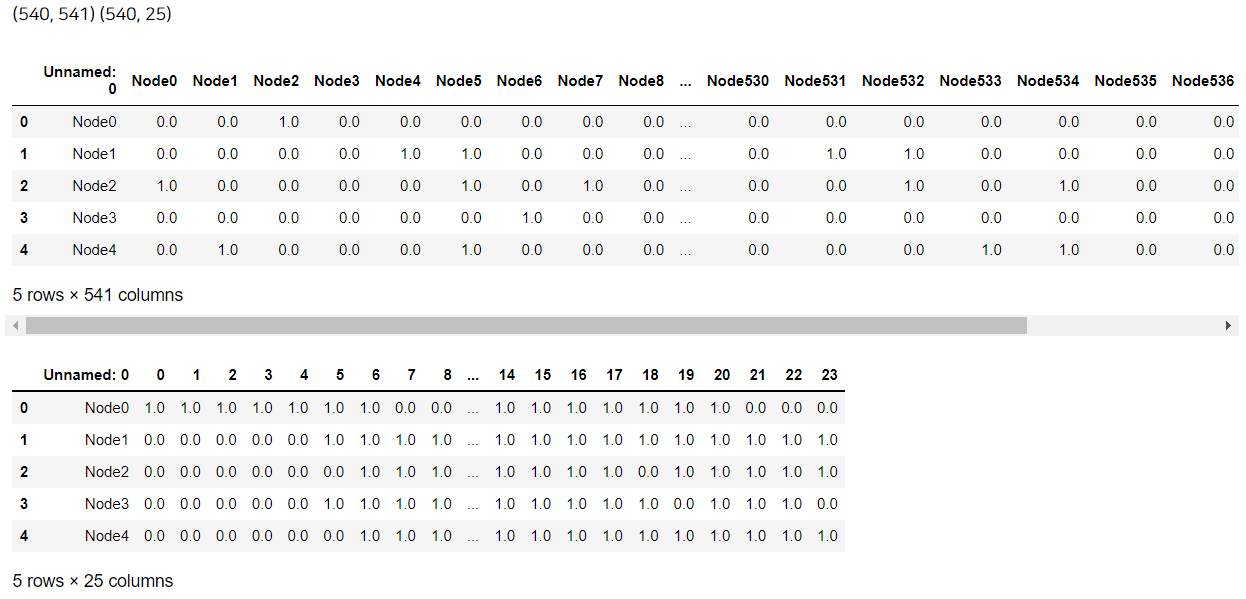
이번 분석에 사용할 데이터 2개, mem_link와 mem_info입니다.
- mem_link: 회원 540명끼리의 SNS 연결상태가 나와 있습니다. 각 회원 이름은 'Node #'로 되어 있습니다. 값이 1이면 연결, 0이면 연결되어있지 않습니다.
- mem_info: 지난 24개월동안의 회원 540명의 쇼핑몰 이용상태가 나와있습니다. 값이 1이면 해당 월에 스포츠센터를 이용, 0이면 이용하지 않았단 뜻입니다.
Tech 77. 링크 수 분포를 시각화하자
앞선 포스팅을 보고 오신 분들은 아시겠지만, 처음엔 20명의 샘플 고객 데이터만 뽑아서 분석을 했었죠. 고객 수가 엄청 많지 않으니 네트워크 시각화를 할 수 있었습니다.
하지만 지금은 540명의 데이터이므로 네트워크로 나타내면 알아보기가 쉽지 않을 것입니다.
그러니 네트워크로 표현하지 말고, 링크(link) 수를 가시화해서 540명의 고객 각각이 연결되어 있는 고객 수가 총 몇명인지를 알아봅시다.
어차피 노드별로 이어져있으면 1, 아니면 0으로 되어있으므로, 각 열의 합계를 구하면 그것이 그 노드(고객)의 연결된 고객 수겠죠?
NUM = len(mem_link.index) #540
array_linkNUM = np.zeros(NUM) #초기화
for i in range(NUM):
array_linkNUM[i] = sum(mem_link["Node" + str(i)]) #각 노드별로 총 몇 명이랑 이어져있을까?
print(array_linkNUM)
이렇게 숫자로만 보니 또 눈에 안 들어오죠. 히스토그램으로 나타내봅시다.
plt.hist(array_linkNUM, bins = 10)
plt.show()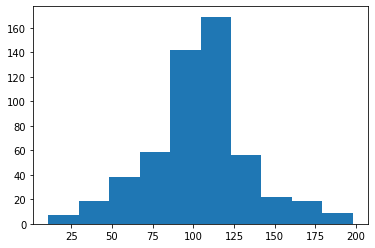
그래프를 보면 링크수가 100에 집중된 정규분포에 가깝습니다.
즉, 540명의 고객은, 연결된 사람 수가 100명 미만이거나 100명 초과인 사람은 적고, 100명 언저리인 사람이 대다수라는 뜻입니다.
그러니 급격히 입소문이 퍼지는 구조는 아니지만, 그렇다고 엄청 많은 사람과 연결된 소수의 인플루언서에만 정보 전파를 의존하고 있지도 않습니다.
Tech 78. 시뮬레이션을 위한 파라미터(확산, 소멸확률)을 추정하자
이 부분은 좀 어렵습니다. 저번 포스팅에선 어떻게 했었나요? 그냥 임의로 확산확률 10%, 소멸확률 5%로 정하고 시뮬레이션을 했었죠.
하지만 이렇게 임의로 확률을 쓰게 되면 좋은 시뮬레이션은 아닙니다. 정확도 높은 시뮬레이션을 위해, 이 확산확률과 소멸확률을 주어진 데이터를 바탕으로 추정해봅시다! (책에서 이 부분 설명이 빈약해서 제 설명을 많이 추가했습니다.)
1. 소멸확률 추정
소멸확률은 어떻게 추정할 수 있을까요?
우리에게 주어진 mem_info를 참고하면, 몇 개월에 이 스포츠 센터를 이용했는지를 알 수 있습니다.
그렇다면 어떤 고객(노드)이 t 시점에는 이용을 했지만(1이지만), 바로 다음 t+1시점에선 이용하지 않은 경우(0인 경우)를 계산해보면 되겠죠!
즉, 식으로 나타내보면 이렇게 될 것입니다.

이 소멸확률을 계산하는 것은 다른 고객과 연결되어 있는지는 고려할 필요가 없습니다. 왜냐하면, 만일 노드 A와 연결이 되어있기 때문에(혹은 안 되어있기 때문에) 노드 B가 t 시점엔 이용하다 t+1 시점엔 이용하지 않는 것이 아니기 때문입니다.
이를 코드로 나타내봅시다.
분모가 count_active, 분자가 count_active_to_inactive입니다. (책에선 반대로 되어있어서 제가 바꿨습니다)
NUM = len(mem_info.index) #540
T_NUM = len(mem_info.columns)-1 #24 (Unnamed가 있어서)
#소멸확률 추정: 노드가 t 시점에는 이용했지만(1) 바로 다음인 t+1 시점에선 이용하지 않을(0일) 확률
count_active = 0
count_active_to_inactive = 0
for t in range(1, T_NUM):
for i in range(NUM):
if (mem_info.iloc[i][t] == 1): #만약 특정 t 시점에서 Node i가 이용한 적이 있다면?
count_active += 1
if (mem_info.iloc[i][t+1] == 0): #그런데 t+1 시점에는 이용한 적이 없다면?
count_active_to_inactive += 1
print(count_active_to_inactive/count_active)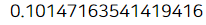
24개월 데이터인 mem_info를 갖고 소멸확률을 추정하면 약 0.1(10%) 가 나옵니다.
2. 확산확률 추정
확산확률 추정은 좀 더 어렵습니다. 그냥 간단하게 생각하면, 아까 전과는 반대로 "특정 노드가 t 시점에선 이용하지 않았지만(0이지만), 바로 다음 t+1 시점에선 이용할(1일) 확률을 구하면 되는 것 아닌가?" 라고 생각할 수 있습니다.
하지만, 소멸확률은 다른 고객과 연결이 되어있는게 딱히 상관이 없었죠. 그러나 확산확률은 안됩니다. 이 스포츠 센터가 입소문으로 전파되기 떄문에 다른 고객과 연결이 되어있는지를 고려해야 합니다.
그렇다고 해서 확산이 되는 게 꼭 다른 고객 때문이리란 법도 없죠. 그냥 다른 사람 추천 받은게 아니라 우연히 검색해서 이용하러 온 것일수도 있잖아요?
그래서 가정이 필요합니다. "전파가 된 이유는 다른 고객과 연결되기 때문으로만 한정한다!" 그럼 이렇게 식을 쓸 수 있습니다.

즉, 이렇게 봅니다.
노드 A와 연결되어 있는 노드 A'에서 t시점엔 이용을 안하다 t+1 시점엔 이용을 했다면 전파가 된 것이라고 봅니다.
그래서 노드 A'이 이용을 안하다 이용을 한 경우를 계산하려면, 노드 A랑 연결이 되어있어야만 한다는 것입니다.
이렇게 보면 A와 연결된 A'에 대해,
count_link를 t시점에 이용을 안 한 횟수, count_link_to_active는 t+1시점엔 이용을 한 횟수(A랑 연결이 되어있기 때문에 A'이 이용을 안했다가 이용한 것으로 봄) 로 나타낼 수 있습니다.
너무 복잡하지만 그래도 어느 정도 감이 잡히시죠? (책에 이런 설명이 전혀 없고 코드만 있어서 이해하느라 좀 고생했습니다ㅠㅠ) 이를 코드로 나타내봅시다.
#확산확률 추정
count_link = 0
count_link_to_active = 0
for t in range(T_NUM -1): #각 t에 대해..
#t 기간에 방문한 적 있는 노드들 (노드 A)
df_link_t = mem_info[mem_info[str(t)] == 1]
#540명 노드의 flag값. 현재는 모두 0으로 초기화되어 있으며,
#만일 t 기간엔 방문안했다 t+1에 방문을 했다면
#기존의 A 노드와 연결이 되어 있기 때문이라 보고, 이를 1로 바꾼다.
temp_flag_count = np.zeros(NUM)
#그리고 df_link_t의 개별 노드 하나씩에 대해서..
for i in range(len(df_link_t.index)):
#노드 A와 연결된 노드 A'들로 df_link_temp 생성
df_link_temp = mem_link[mem_link['Node' + str(df_link_t.index[i])] == 1]
for j in range(len(df_link_temp.index)):
#A' 들이 t기간에 방문을 안했니?
if (mem_info.iloc[df_link_temp.index[j]][str(t)] == 0):
#그리고 A' 들이 temp_flag_count 값이 0이니? (디폴트값)
if (temp_flag_count[df_link_temp.index[j]] == 0):
#그렇다면 count_link를 1씩 추가
count_link += 1
#그렇다면 A'들이 t+1 기간엔 방문을 했니?
if (mem_info.iloc[df_link_temp.index[j]][str(t+1)] == 1):
#그리고 A' 들이 temp_flag_count 값이 0이니? (디폴트값)
if (temp_flag_count[df_link_temp.index[j]] == 0):
#그렇다면 A' 노드 번호인 temp_flag_count 값은 1로 변경하고
temp_flag_count[df_link_temp.index[j]] = 1
#count_link_to_active를 1씩 추가
count_link_to_active += 1
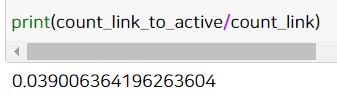
print(count_link_to_active/count_link)
너무 복잡하지만 차근차근 설명해보겠습니다.
우선 t 시점에 이용한 적이 있는 노드A를 'df_link_t'라고 합니다. 또한 A와 연결된 노드 A'는 'df_link_temp'입니다. (얘는 t시점엔 0이었다가, t+1 시점엔 전파가 되어 1이 되었는지를 계산함)
그래서 각 노드 A에 대해, A'이 t 시점에 이용한 적이 없다면 count_link를 1씩 더하며, A'이 t+1 시점엔 이용을 했다면 count_link_to_active 값을 1씩 더합니다.
어차피 mem_info, mem_link의 인덱스는 모두 노드 번호이기 때문에, temp_flag_count 값을 NUM 값으로 초기화시켜도 됩니다. 전부 540개로 통일!
그래서 temp_flag_count의 각 원소는 노드라고 보면 됩니다. 개별 노드가 t시점엔 이용을 안했다가 t+1 시점엔 이용하게 될 경우 1로 바꿉니다.
그리고 사실 이 확산확률을 구하기 위해서 중요한 것은 count_link와 count_link_to_active지, temp_flag_count가 아닙니다. 그래서 이 부분은 이해가 안된다면 안하셔도 괜찮을 것 같습니다.
이렇게 해서 구한 확산확률은 다음과 같습니다. 약 4%네요.
오늘은 이 파라미터들(확산확률, 소멸확률)을 추정하는 데 많은 양을 할애했네요.ㅎㅎ
다음 포스팅에선 이 추정한 파라미터를 갖고 시뮬레이션을 해보겠습니다. 그리고 이 시뮬레이션 결과를 실제 결과와 비교해봅니다. 감사합니다 :)
'Data Science > Analysis Study' 카테고리의 다른 글
| Python OpenCV (1) - 이미지, 동영상 데이터를 불러오고 저장하기 (0) | 2022.05.11 |
|---|---|
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (4) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.05 |
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (2) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.03 |
| 파이썬 시뮬레이션 - SNS 입소문 전파 예측하기 (1) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.05.02 |
| 물류 네트워크 최적화 설계 예제 (python logistics_network) / 파이썬 데이터 분석 실무 테크닉 100 (0) | 2022.04.30 |




